問題編
このページは計算尺の問題・パズルを扱います。
ヒントを見る場合は、マウスでなぞってテキストを選択状態にしてください。
- ■問題1 「立方根」
-
- 72.5^(1/3) を計算しなければなりませんが、あいにく手元には古いマンハイム計算尺
- A [ B, C ] D // [ S(A), L, T ]
- しか、ありません。 K尺が無いのが痛いです。
- もちろん L尺を使った計算はできますが、何とか表側の尺度(A, B, C, D)だけで計算できないでしょうか?
-
- ■問題2 「5乗根」
-
- 18.02 の 5 乗根 18.02^(1/5) を ヘンミ No.40RK の表側の尺度 (A, B, C, CI, D, K) だけを使用して求めてください。
- ただし、滑尺による数値のセットは 1回のみでお願いします。 カーソルはどれだけ動かしても構いません。
-
- 《ヒント1》 なぜ「滑尺操作は 1回のみ」と言ってないのでしょう?
- 《ヒント2》 あることをしないとカーソルが 2つ必要。
-
- ■問題3 「7乗根」
-
- 7.36^(1/7) ( 7.36 の 7乗根) を計算してください。 ただし、手元にはヘンミの P24 (DF[CF,CI,C]D,A) しかありません。
どうやりますか?
- 《ヒント1》 C尺とD尺だけで可能です。
- 《ヒント2》 忍耐力が必要です。
-
- ■問題4 「入れ子の正三角形」
-
- ISRG で出題された図形問題です。
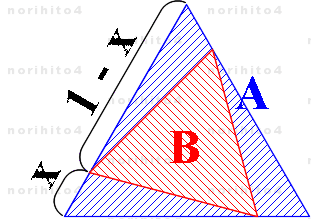
- 図のように重なった 2つの正三角形 A, B があります。
- B の面積は A の面積の 1/2 です。
- A の各辺は B の各頂点と接してます。
- A の各辺は、長さを 1 としますと、 B の各頂点によって、 x と 1-x に分割されてます。
- x , 1-x の長さはどれだけでしょうか?
-
-
-
- 《ヒント1》 正三角形 A と B で形成された 小さな細長い三角形の面積は正三角形 A の面積の 1/6 です。
- 《ヒント2》 計算尺は方程式を解くのに使います。
-
- ※ ISRG では今まで数多くの図形問題が出題されてます。 しかしながら、その回答は必ずしも計算尺を使って示されるとは限りません。
- この問題のときも、解答者は数式を展開するだけで解答し、出題者もそれを褒めるだけでした。
- 出題者は、本当は、計算尺を使った解答が欲しかったに違いありません。
-
- ■問題5 「 x を求めよ」
-
- ログ・ログ・デュープレックス(例えば、ヘンミ 259D, 260, リコー 151系) を使用して、次式の x を求めてください。
ただし、cos x の x は度(deg.)で、 x は 0 〜 360 deg. とします。 答えは 3つありますが、取り敢えずは、
0 〜 90 deg. にある 2つでも構いません。
- 微小角と呼ばれる範囲( 0 〜 6 deg. , 84 〜 96 deg. 等) には答えはありませんので、ST尺等は使用しません。
ただし、かなり近い箇所に答えが 1つあります。
-
- x * e ^ ( 1.57 * cos x ) = 100
-
- 《ヒント1》 ヘンミ 258 (POST 1460 Versalog) のような計算尺が一番この問題向きです。
上に上げた計算尺の場合、あることをしないとイライラします。
- 《ヒント2》 ヘンミ 254系, 149A も、《ヒント1》に加えてあることをすれば可能です。
- 《ヒント3》 ヘンミ P261 ではおそらく無理でしょう。
-
- ※ ISRG で出題されていた問題ですが、数値を一部変更しています。
- (元の問題は ISRG のメッセージで解答が出てます。)
- ※ x が deg. というのは何か気持ち悪いですよね。 計算尺のための独特の問題と言えるでしょう。
- ※ ヒントを 3つも並べましたが、あまり意味はないかもしれません。
- こういう問題は実際に計算尺をあれこれいじくって答えを導くのが楽しみってものです。
-
- ■問題6 「水平線まで何キロ?」
-
- 砂浜の波打ち際に立って、水平線を見ている人がいます。 この人が立っている場所から水平線まで何 km あるでしょう?
- ただし、地球は半径 6370 km の球体、海面・波打ち際の海抜(標高)は 0 m 、見ている人の目の高さは 1.5 m とします。
-
- ※ おそらく、2つの方法が考えられますが、両方やってみることをおすすめします。
- (1)角度を使わないピタゴラスの定理を利用。
(【目から水平線の直線距離】≒【立ってる所から水平線までの地球の円周上の距離】 として直線距離を計算。)
- (2)【立ってる所から水平線までの地球の円周上の距離】
= 【地球の半径】×【立ってる所から水平線までの地球の中心角度(ラジアン)】 として海面の曲線距離を計算。
-
- ※ 熱血平成教育予備校(2007/09/02)というTV番組の中での話題(問題ではありません)からの出典です。
山の上から見ている訳ではありませんので、意外に近いです。
- ※ (1)の方が簡単です。 (2)では、「微小角」・「1に極めて近い数の逆数」といった、
通常、計算尺で計算できる範囲外の計算が必要なのでかなりタフです。
数学公式集があると便利です。
- ※ (1),(2) とも、『どうして、そう見なせるのか?』 ,『何が無視できるか?』 という感覚が重要かもしれません。
- 改版メモ
- 2007/09/18 : 問題5,6 追加。
- 2007/06/04 : 初版(取り敢えず版)
