C,D尺だけで n乗根

　数値 a の n 乗根 a^(1/n) を C,D尺だけで求めます。

　ここでは、取り敢えず、 a は 1 ～ 10 の実数,　n は 2～10 程度の範囲の自然数とします。

　

　まず、実践の前にマンハイム計算尺に代表される一般の対数尺について考えてみます。

　通常、n=2, 3 の場合（平方根, 立方根）は以下のような操作です。

h>A[a] → D[a^(1/2)] ,　　h>K[a] → D[a^(1/3)]

　A尺は D尺の 1/2, K尺は D尺の1/3 に圧縮された尺度です。

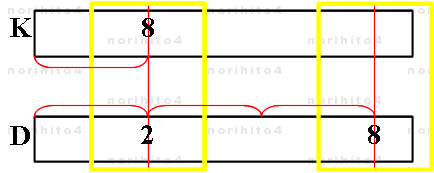
　a = 8 , n = 3 の時、すなわち、8 の立方根 8^(1/3) = 2 について図示しますと、下図のようになります。

　

　D尺上の "8" の位置は、左基線から "2" までの距離の 3 倍の距離にあります。

　この図から、まず、n乗を C, D尺のみで計算する方法が見えたと思います。

　そして、もう勘の良いみなさんは n乗根の計算方法もお気づきになり、恐怖を覚えたことでしょう。

　

　そう、今、あなたは腕時計に付いているような C尺, D尺のみの計算尺しか持ってません。そんな状況で上の例の "2" のような数値を見つけなければならないのです。（カーソルがあることに感謝しなければなりません。）

　

　では、この CD計算尺で a の n 乗根 x = a^(1/n) を求める手順を示します。

　

【1】 h>D[a]　：　カーソルを D尺の a に合わせます。

【2】 D尺左基線からカーソル線の位置 a までの距離の 1/n の距離を目分量で得て、
　　x0 とし、覚えておきます。

【3】 h>D[x0]　：　カーソルを D尺の x0 に合わせます。

【4】 C[l-i]>h　：　C尺左基線（=1）をカーソルに合わせます。

【5】 h>C[x0]　：　カーソルを C尺 x0 に合わせます。

【6】【4】～【5】を n-1 回繰り返します。

【7】最後のカーソル操作の後、カーソル線下の D尺に x0^n を得ます。
　　これが運良く a に一致したら、 x0^n = a すなわち、 x0 = x = a^(1/n) で、終わりですが、
　　一致しない場合は、x0^n と a の差の 1/n を目分量や、カーソル線・ C尺の目盛を参照して得て、
　　新たな x0 を設定し、【3】～【6】を再度行います。

【8】 x0^n = a となるまで【7】を繰り返します。

※ 途中で、「俺、何やってんだろう？」とか、「何か昔の女に会いたくなってきたな・・・」とか、思ってはいけません。

　・・・と、いうことでこの技（？）の正体は端的に言えば試行錯誤 (Trial and Error) でした。

　何の役に立つのでしょうか？おそらく全く実用的ではありませんが、「計算尺の原理の勉強」や、「目分量の訓練」, 「空間把握の訓練」としてはどうでしょう。

　

　関数キーの無い電卓でも同様の手法が使えますが、x の初期値 x0 を採るときに、対数 log x が log a の 1/n であることがビジュアル的にある程度見当がつく計算尺の方が有利かも知れません。

　

■ a の範囲が 1 ～ 10 以外の場合は？　

　

　通常の A尺, K尺を使用した平方根, 立方根の計算と同様な配慮が必要です。

　例えば、 356^(1/7) （a=356, n=7）の場合は、まず a=3.65 の場合と同様に D尺 3.56 にカーソルを置きます。

　左基線の左側に D尺がさらに 2サイクル続いているとイメージし、合計 3 サイクル分の D尺（巨大 K尺）イメージ内で 365 の 1/7 の値 x0 の見当をつけます。

　後はまた、a の範囲が 1 ～ 10 の場合と同様に実在の D尺上で【3】～【8】の手順を踏みますが、適切な x0 が得られた場合は、途中 2 回の基線の置き換えがあるはずです。