屆乮偄偵偟偊乯偺寁嶼広偺埵庢傝婰崋
丂
儅乕僋丒婰弎
宖嵹埵抲
| 愢柧
|
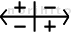
屌掕広
乮忋懁乯
A広偺
嵍塃
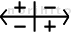
屌掕広
乮忋懁乯
A広偺
嵍塃
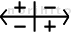
屌掕広
乮忋懁乯
A広偺
嵍塃
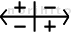
屌掕広
乮忋懁乯
A広偺
嵍塃
|
- 丂A,B広偵傛傞忔彍嶼乮*1乯偵偍偄偰丄彫悢揰埵抲傪寛掕偡傞偨傔偺曽朄傪恾幃壔偟偨傕偺偱奺晹偼埲壓偺僀儊乕僕偱偁傞丅
- 丂
- 丂
 廲慄 丗 廲慄 丗
- 丂忔彍嶼偺奺悢抣偺彫悢揰埵抲傪帵偡丅
- 丂
 墶慄 丗 墶慄 丗
- 丂暘悢偺墶慄偺僀儊乕僕偱偁傝丄忔彍嶼傪暘悢宍幃偺忔嶼偲偟偨偲偒偵丄暘巕懁偺悢抣傪忋偵丄暘曣懁偺悢抣傪壓偵尒棫偰傞丅
- 丂
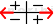 栴報 丗 栴報 丗
- 丂奺悢抣傪寁嶼広偵僙僢僩偡傞嵺偵彫悢揰乮廲慄乯傪堏摦偡傞曽岦傪帵偡丅
- 丂
 亄亅偺儅僩儕僋僗 丗 亄亅偺儅僩儕僋僗 丗
- 丂悢抣傪寁嶼広偵僙僢僩偡傞嵺偺彫悢揰堏摦偑丄摎偊偺埵庢傝偺憹尭偵偳偆斀塮偝傟傞偐傪帵偡儅僩儕僋僗丅
丂椺偊偽丄 乬 x 亐 y = x / y 乭 偺 y 傪 B 広偵僙僢僩偡傞嵺偵彫悢揰埵抲傪嵍乮仼乯偵 2寘堏摦偟偨応崌偼丄
y 偼暘曣懁乮墶慄偺壓懁乯側偺偱丄儅乕僋偺嵍壓偺晞崋 乬亅乭 偑懳墳偟丄A広偵摼傜傟傞摎偊偵 -2寘暘偺塭嬁傪梌偊傞丅
- 丂
- 丂偲丄愢柧偟偰傕 乽壗偺偙偭偪傖乿 側偺偱丄埲壓偵忔嶼丒彍嶼偺椺傪僨僔儅儖億僀儞僩僀儞僕働乕僞乕
乮埲壓扨偵僀儞僕乕僞乕偲棯偡乯偺憖嶌傕岎偊偰堦偮偢偮帵偡丅
- 丂
- 椺1丗 234亊345 = 80700 乮恀抣 80730乯
- 丂
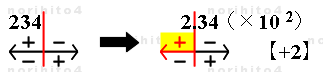
- 丂傑偢丄 234 偺彫悢揰傪嵍乮仼乯偵 2寘堏摦偟丄 2.34 偱偺寁嶼傪峫偊傞偲丄
 丂 丂
- 丂偲側傞偺偱丄僀儞僕働乕僞乕偺恓愭傪亄懁偺 2 乮+2乯偵崌傢偣丄僇乕僜儖慄傪 A広乮塃椞堟乯 2.34 偵堏摦偡傞丅
 丂 丂
- 丂
- 丂師偵丄 345 偺彫悢揰傕嵍乮仼乯偵 2寘堏摦偟丄 3.45 偲偟偰寁嶼広偵愝掕偡傞丅
- 丂傑偨丄 嵍乮仼乯偵 1寘偩偗堏摦偟偨 34.5 偺応崌傕堦弿偵峫偊偰傒傞丅 乮*2乯
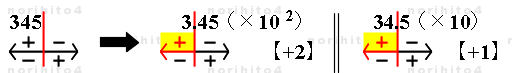 丂 丂
- 丂傛偭偰丄丄寁嶼広偵 3.45 偲偟偰僙僢僩偡傞応崌偼 僀儞僕働乕僞偺恓愭傪 +2 偟偰 +4 偺埵抲偵丅
- 丂傑偨丄34.5 偲偟偰僙僢僩偡傞応崌偼 +1 偟偰 +3 偺埵抲偵偡傞丅
- 丂偦偟偰丄婎慄朄乮=僇乕僜儖朄乯偱忔嶼傪峴偆偺偱丄妸広傪摦偐偟偰 B広嵍婎慄傪僇乕僜儖慄乮A広 2.34乯偵崌傢偣偨屻丄
僇乕僜儖慄傪 B広 3.45 傑偨偼 34.5 偵崌傢偣傞偲丄僇乕僜儖慄壓 A広偵 8.07 傑偨偼 80.7 偑摼傜傟傞丅
 丂 丂
- 丂傛偭偰丄摎偊偼 8.07亊10 +4 = 80.7亊10 +3 = 80700 偲媮傔傜傟傞丅
- 丂
- 丂
- 椺2丗 0.876亐432 = 0.00203 乮0.00202777丒丒丒乯
- 丂
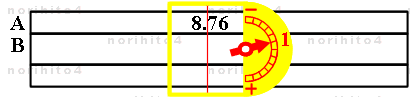
- 丂傑偢丄0.876 偺彫悢揰傪塃乮仺乯偵 1寘堏摦偟丄 8.76 偲偟偰 A広偵抲偔偲偡傞偲丄
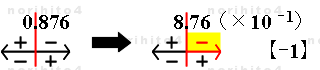 丂 丂
- 丂偲側傞偺偱丄僀儞僕働乕僞乕偺恓愭傪亅懁偺 1 乮-1乯 偵崌傢偣丄僇乕僜儖慄傪 A広 8.76 偵崌傢偣傞丅
 丂 丂
- 丂
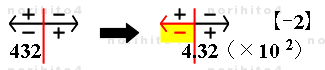
- 丂師偵丄 432 偺彫悢揰傪嵍乮仼乯偵 2寘堏摦偟丄 4.32 偲偟偰寁嶼偡傞丅 栤戣幃偼 0.876亊 1/432
偲彂偒姺偊傜傟傞偺偱丄432 偼婰崋偺暘曣懁偺亄亅儅僩儕僋僗偱峫偊傞偙偲偵側傞丅
 丂 丂
- 丂傛偭偰丄僀儞僕働乕僞乕偺恓愭傪 -2 偟偰 -3 偺栚惙偵崌傢偣丄妸広傪摦偐偟偰 B広 4.32 傪僇乕僜儖慄乮A広 8.76乯
偵崌傢偣傞偲丄妸広婎慄埵抲偺 A広偵 2.03 偑摼傜傟傞丅
 丂 丂
- 丂
- 丂A広忋偺摎偊 2.03 偲僀儞僕働乕僞乕偺 -3 偐傜丄嵟廔揑側摎偊 2.03亊10-3 = 0.00203 偑媮傔傜傟傞丅
|
Quot.
+1
乮Q+1乯
屌掕広
乮壓懁乯
D広偺嵍
Quot.
+1
乮Q+1乯
屌掕広
乮壓懁乯
D広偺嵍
Quot.
+1
乮Q+1乯
屌掕広
乮壓懁乯
D広偺嵍
Quot.
+1
乮Q+1乯
屌掕広
乮壓懁乯
D広偺嵍
|
- 丂C,D広偵傛傞彍嶼乮拞崌傢偣朄=妸広朄乯偺嵺偵埵庢傝傪寛掕偡傞偨傔偺僈僀僪偱偁傞丅
- 丂偙偺棯崋偺捈栿偼 亀彜 乮quotient乯 偵 1傪壛偊側偝偄亁偱偁傞偑丄
寁嶼広偺嵍抂偵偁傞偙偲偵傕堄枴偑偁傝丄壓婰偺傛偆側偙偲傪昞偟偰偄傞丅
- 丂
- 丂彜乮quotient丟妱傝嶼偺摎偊乯偺寘悢偼丒丒丒丂
- 丂
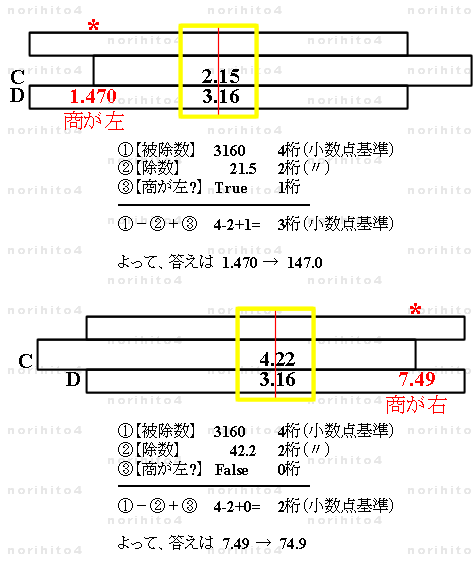
- 嘆 D広忋偱丄彜偑旐彍悢乮dividend丟妱傜傟傞悢乯傛傝嵍懁偵偁傞偲偒偼丄
丂旐彍悢偺寘悢偐傜彍悢乮divisor丟妱傞悢乯偺寘悢傪堷偄偨傕偺偵 1寘壛偊偨悢偲側傞丅
- 丂
- 丂亂彜偺寘悢亃 亖 亂旐彍悢偺寘悢亃亅亂彍悢偺寘悢亃亄 1
- 丂
- 嘇 D広忋偱丄彜偑旐彍悢傛傝塃懁偵偁傞偲偒偼丄
丂旐彍悢偺寘悢偐傜彍悢偺寘悢傪堷偄偨悢偲側傞丅
- 丂
- 丂亂彜偺寘悢亃 亖 亂旐彍悢偺寘悢亃亅亂彍悢偺寘悢亃
- 丂
- 丂埲壓偵丄娙扨側椺傪帵偡丅
- 丂
- 椺丗丂3160亐21.5 = 147.0 ,丂3160亐42.2 = 74.9丂
- 丂
- 丂
- 仸楢懕彍嶼
- 丂
- 丂楢懕偟偰妱傝嶼傪峴偆応崌偺埵庢傝傕摨條偱丄
妱傝嶼偺憖嶌偺搒搙丄怴偟偄彜偑偦傟傑偱偺彜偺嵍偵偁傞応崌傪僇僂儞僩偟偰偍偒丄
嵟廔揑側夞悢傪場巕偺寘悢偺堷偒嶼寢壥偵壛偊傟偽傛偄丅
- 丂怴偟偄彜偑偦傟傑偱偺彜偺嵍偵偁傞偲偄偆忬懺偼丄尵偄姺偊傟偽丄
妸広偑屌掕広偐傜塃偵堷偒弌偝傟偨乮撍偒弌偨乯忬懺偱偁傝丄偙偺忬懺偑惗偠偨嵺偵 +1 傪僇僂儞僩偟偰偄偗偽傛偄丅
- 丂僇僂儞僩偺庤抜偲偟偰丄埵庢傝僇乕僜儖偺僨僔儅儖億僀儞僩僀儞僕働乕僞乕乮埲壓扨偵僀儞僕働乕僞乕偲棯偡乯
偺棙梡傕桳岠偱偁傞丅
- 丂
- 椺丗丂156亐17亐21亐134 = 0.00326
- 丂
- 丂堦楢偺憖嶌傪僟僀儎僌儔儉偱昞帵偡傞偺偼僗儁乕僗傪偲傞偺偱丄僥僉僗僩乮儔僐僯僘儉乯偱帵偡丅
- 丂
- 丂(1) 寁嶼広憖嶌乮妸広塃撍弌偟忬懺傪亂Q+1亃偱昞帵丅 僀儞僕働乕僞乕傪 +1 偟傑偡丅乯
- 丂
- h>D[1.56] C[1.7]>h h>sl[r.i] C[2.1]>h亂Q+1亃
h>[l.i] C[1.34]>h亂Q+1亃
丂仺 D[3.26]@h
- 丂
- 丂(2) 寘悢寁嶼乮彫悢揰婎弨乯
- 丂
- 丂3寘 - 2寘 -2寘 +1 -3寘 +1 = -2寘
- 丂
- 丂(1), (2)傛傝丄摎偊偼
- 丂
- 丂0.00326
|
Prod.
-1
乮P-1乯
屌掕広
乮壓懁乯
D広偺塃
Prod.
-1
乮P-1乯
屌掕広
乮壓懁乯
D広偺塃
Prod.
-1
乮P-1乯
屌掕広
乮壓懁乯
D広偺塃
Prod.
-1
乮P-1乯
屌掕広
乮壓懁乯
D広偺塃
|
- 丂C,D広偵傛傞忔嶼乮婎慄朄=僇乕僜儖朄乯偺嵺偵埵庢傝傪寛掕偡傞偨傔偺僈僀僪偱偁傞丅
- 丂儅乕僋偺捈愙揑側堄枴偼 亀愊 乮product乯 偐傜 1傪尭偠側偝偄亁偱偁傞偑丄寁嶼広偺塃抂偵偁傞偙偲偵傕堄枴偑偁傝丄
壓婰偺傛偆側偙偲傪昞偟偰偄傞丅
- 丂
- 丂愊乮product丟妡偗嶼偺摎偊乯偺寘悢偼丒丒丒丂
- 丂
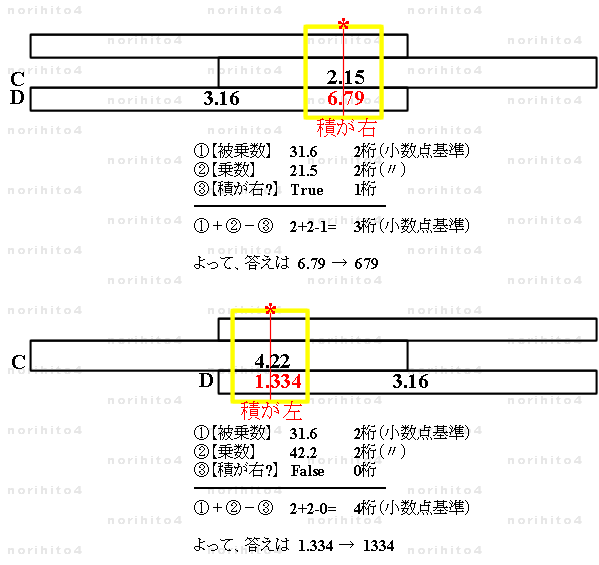
- 嘆 D広忋偱丄愊偑旐忔悢乮multiplicand丟妡偗傜傟傞悢乯傛傝塃懁偵偁傞偲偒偼丄
丂旐忔悢偺寘悢偵忔悢乮multiplier丟妡偗傞悢乯偺寘悢傪壛偊偨傕偺偐傜 1寘尭偠偨悢偲側傞丅
- 丂
- 丂亂愊偺寘悢亃 亖 亂旐忔悢偺寘悢亃亄亂忔悢偺寘悢亃亅 1
- 丂
- 嘇 D広忋偱丄愊偑旐忔悢傛傝嵍懁偵偁傞偲偒偼丄
丂旐忔悢偺寘悢偵忔悢偺寘悢傪壛偊偨悢偲側傞丅
- 丂
- 丂亂愊偺寘悢亃 亖 亂旐忔悢偺寘悢亃亄亂忔悢偺寘悢亃
- 丂
- 丂埲壓偵丄娙扨側椺傪帵偡丅
- 丂
- 椺丗丂31.6亊21.5 = 679乮恀抣 679.4乯 ,丂31.6亊42.2 = 1334乮恀抣 1333.52乯丂
 丂 丂
- 丂
- 仸楢懕忔嶼
- 丂
- 丂楢懕偟偰妡偗嶼傪峴偆応崌偺埵庢傝傕摨條偱丄
妡偗嶼偺憖嶌偺搒搙丄怴偟偄愊偑偦傟傑偱偺愊偺塃偵偁傞応崌傪僇僂儞僩偟偰偍偒丄
嵟廔揑側夞悢傪場巕偺寘悢偺懌偟嶼寢壥偐傜尭偢傟偽傛偄丅
- 丂怴偟偄愊偑偦傟傑偱偺愊偺塃偵偁傞偲偄偆忬懺偼丄尵偄姺偊傟偽丄
妸広偑屌掕広偐傜塃偵堷偒弌偝傟偨乮撍偒弌偨乯忬懺偱偁傝丄偙偺忬懺偑惗偠偨嵺偵 -1 傪僇僂儞僩偟偰偄偗偽傛偄丅
- 丂僇僂儞僩偺庤抜偲偟偰丄埵庢傝僇乕僜儖偺僨僔儅儖億僀儞僩僀儞僕働乕僞乕乮埲壓扨偵僀儞僕働乕僞乕偲棯偡乯
偺棙梡傕桳岠偱偁傞丅
- 丂
- 椺丗丂15.6亊17亊2.1亊1.34 = 746 乮恀抣 746.2728乯
- 丂
- 丂堦楢偺憖嶌傪僟僀儎僌儔儉偱昞帵偡傞偺偼僗儁乕僗傪偲傞偺偱丄僥僉僗僩乮儔僐僯僘儉乯偱帵偡丅
- 丂
- 丂(1) 寁嶼広憖嶌乮妸広塃撍弌偟忬懺傪亂P-1亃偱昞帵丅 僀儞僕働乕僞乕傪 -1 偟傑偡丅乯
- 丂
- h>D[1.56] sl[l.i]>h亂P-1亃 h>C[1.7] sl[l.i]>h亂P-1亃
h>C[2.1] sl[l.i]>h亂P-1亃 h>C[1.34]
丂仺 D[7.46]@h
- 丂
- 丂(2) 寘悢寁嶼乮彫悢揰婎弨乯
- 丂
- 丂2寘 -1 + 2寘 -1 + 1寘
-1 + 1寘 = 3寘
- 丂
- 丂(1), (2)傛傝丄摎偊偼
- 丂
- 丂746.
|
Quot.
+1
乮Q+1乯
丆
Prod.
-1
乮P-1乯
偺曗懌
|
- 仭楢懕忔彍寁嶼
- 丂
- 丂C, D広偵偰忔彍崿崌偺楢懕寁嶼傪峴偆応崌偺埵庢傝傕丄楢懕忔嶼丒楢懕彍嶼偲摨條偱偁傞丅
- 丂憖嶌偺搒搙丄妡偗嶼側傜場巕偺寘悢傪壛嶼偟丄妱傝嶼側傜場巕偺寘悢傪尭嶼偡傞丅
- 丂偦偟偰丄妸広偑塃偵撍偒弌傞憖嶌偺嵺偵丄偦傟偑妡偗嶼側傜 -1 丆妱傝嶼側傜 +1 偟偰偄偒丄
嵟屻偵場巕偺寘悢寁嶼寢壥偺挷惍傪峴偆丅
- 丂僇僂儞僩偵偼傕偪傠傫埵庢傝僇乕僜儖偺僨僔儅儖億僀儞僩僀儞僕働乕僞乕偑棙梡偱偒傞丅
- 丂
- 仭埵庢傝
- 丂
- 丂C, D広偺忔彍偱偺埵庢傝偼丄A, B広偺忔彍偱偺埵庢傝偲堘偄丄婎杮揑偵彫悢揰傪婎弨偲偟偨愨懳揑側寘乮span乯傪峫偊傞丅
- 丂
丂
| 悢抣
| 寘(span)
|
123.
12.3
丂 1.23
丂 0.123
丂 0.0123
丂 0.00123
丂 0.000123
| 3
2
1
0
-1
-2
-3
|
丂
- 丂
- 仭Quot.+1 , Prod.-1 偺暿昞尰
- 丂
- 丂乬Quot.+1乭 丆乬Prod.-1乭 偼丄 乬Q+1乭 丆乬P-1乭 偲偄偭偨徣棯僶乕僕儑儞偑偁傞偑丄
寁嶼広偵傛偭偰偼偝傜偵徣棯偝傟丄扨偵 乬亄乭 丆乬亅乭 偲昞婰偝傟偰偄傞傕偺傕偁傞丅
- 丂偙傟傜偺昞婰偼偡傋偰 亀彜丒愊偑旐彍悢丒旐忔悢偵懳偟偰偳偪傜偵偁傞偐亁 偄偆堄枴偱嵍塃偵怳傝暘偗傜傟偰偄傞偑丄
妸広偑塃偵堷偒弌偝傟偨帪偵 乬Quot.+1乭 丆乬Prod.-1乭 偑敪惗偡傞偙偲偐傜丄
亀妸広偑偳偪傜偵堷偒弌偝傟偰偄傞偐亁 偲偄偆偙偲偱嵍塃偵埵庢傝憖嶌偺巜帵傪昞婰偟偰傕椙偄偼偢偱偁傞丅
- 丂嫵杮偺拞偵偼丄妸広偑堷偒弌偝傟偨曽岦偵埵庢傝憖嶌偺巜帵傪彂偒崬傓偙偲傪悇彠偟偰偄傞傕偺傕偁傝丄
椺偊偽丄嵍懁偵乬亊亖SUM乭 丆乬亐亖DIFF.乭丄 塃懁偵乬亊亖SUM亅1乭 丆乬亐亖DIFF.亄1乭
偲昞婰偡傞丅
- 丂
丂
| 嵍偺昞帵
| 塃偺昞帵
| 嵍塃偺堄枴
|
Quot.+1
Q+1
亄
亊亖SUM
亐亖DIFF.
| Prod.-1
P-1
亅
亊亖SUM亅1
亐亖DIFF.亄1
| 彜丒愊偺旐彍悢丒旐忔悢偵懳偡傞曽岦
妸広偑堷偒弌偝傟偰偄傞曽岦
|
丂
|

