<style>
v\:* { behavior: url(#default#VML) }
o\:* { behavior: url(#default#VML) }
.shape { behavior: url(#default#VML) }
</style>
<![endif]--><!--[if gte mso 9]>
<xml><o:shapedefaults v:ext="edit" spidmax="1027"/>
</xml><![endif]-->
ジョウの尖端に '◆' ハンドルを設定し、 これを左右に移動することにより、ジョウの開閉とデプスの伸縮を意図してます。
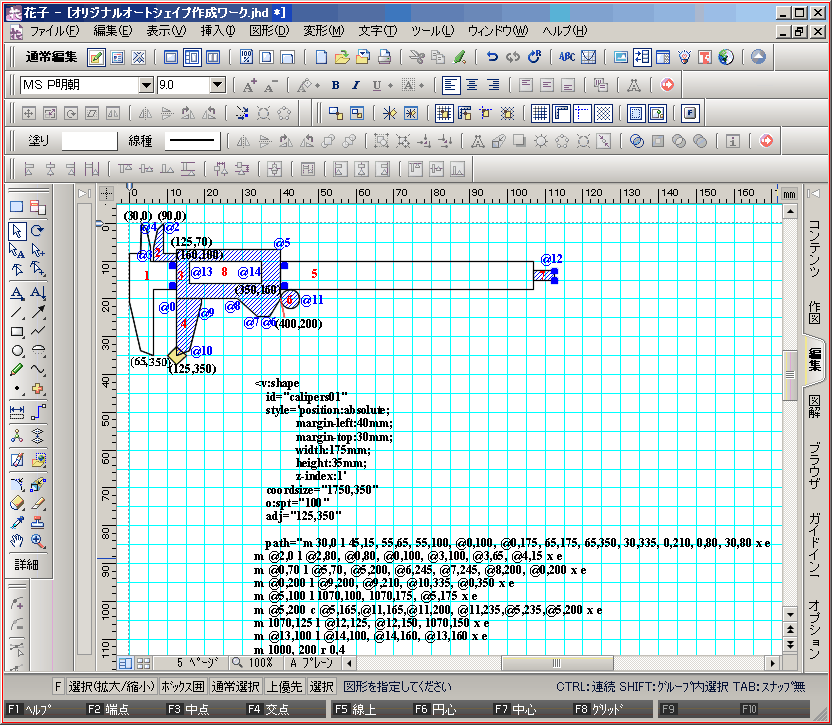
3年ほど前(2006年)、何もわかってない状態で勢いだけで作成した コッパズカシイ例ですが、何かのお役に立てば幸いです。(何もわかってないのは今も同じ…)
id="calipers01"
style='position:absolute;
margin-left:10mm;
margin-top:5mm;
width:175mm;
height:35mm;
z-index:1'
coordsize="1750,350"
o:spt="100"
adj="125,350"
path="m 30,0 l 45,15, 55,65, 55,100, @0,100, @0,175, 65,175, 65,350, 30,335, 0,210, 0,80, 30,80 x e
m @2,0 l @2,80, @0,80, @0,100, @3,100, @3,65, @4,15 x e
m @0,70 l @5,70, @5,200, @6,245, @7,245, @8,200, @0,200 x e
m @0,200 l @9,200, @9,210, @10,335, @0,350 x e
m @5,100 l 1070,100, 1070,175, @5,175 x e
m @5,200 c @5,165,@11,165,@11,200, @11,235,@5,235,@5,200 x e
m 1070,125 l @12,125, @12,150, 1070,150 x e
m @13,100 l @14,100, @14,160, @13,160 x e
m 1000, 200 r 0,4 t 0,-2 r 2,0 t 0,-2 r 0,4 t 2,0 r 0,-4, 2,4, 0,-4 nf e
t 1,3 r 1,-1, 1,1, -1,1 x nf e
t 2,0 r 0,-2, 1,0 t 1,0 r -1-1, 1,-1, 1,1, -1,1, 0,2 nf e"
fill="false">
<v:formulas>
<v:f eqn="val #0"/>
<v:f eqn="val #1"/>
<v:f eqn="sum @0 0 35"/>
<v:f eqn="sum @0 0 60"/>
<v:f eqn="sum @0 0 50"/>
<v:f eqn="sum @0 275 0"/>
<v:f eqn="sum @0 245 0"/>
<v:f eqn="sum @0 215 0"/>
<v:f eqn="sum @0 160 0"/>
<v:f eqn="sum @0 65 0"/>
<v:f eqn="sum @0 35 0"/>
<v:f eqn="sum @0 325 0"/>
<v:f eqn="sum @0 1000 0"/>
<v:f eqn="sum @0 35 0"/>
<v:f eqn="sum @0 225 0"/>
</v:formulas>
<v:handles>
<v:h position="#0,#1" xrange="125,750" yrange="350,350" />
</v:handles>
</v:shape>
- position : オートシェイプの位置の指定の仕方で、取り敢えずは絶対位置 absolute で指定。
- margin-left : ウィンドウの左端からオートシェイプの左端までの距離を mm や pt などの単位で指定。
- margin-top : ウィンドウの上端からオートシェイプの上端までの距離を mm や pt などの単位で指定。
- width : オートシェイプの幅を mm や pt などの単位で指定。
- height : オートシェイプの高さを mm や pt などの単位で指定。
- z-index : オブジェクトを重ねるときの順番の指定ですが、取り敢えず '1' とかにしておきましょう。
- margin-left : ウィンドウの左端からオートシェイプの左端までの距離を mm や pt などの単位で指定。
- (別の数値にしても自動的に 100 になる可能性大。)
- パラメータは 8つまで指定できます。
- 座標値は width や height で指定した領域の外の座標でも OK です。
- 下記に各コマンドについて簡単に説明しますが、詳細は W3C の VMLドキュメント path エレメントの項などを参照願います。
命令(名称) 例 説明 m (moveto) m 0,0 ・ 新しいサブパス(一連の描画)の開始点を (x, y) 座標で指定します。
・ 指定はオートシェイプ内部の絶対座標です。
・ パラメータは "x 座標値, y 座標値" の 2つのみです。
※ このコマンドに限らず、座標の指定は width や height の範囲外
でも OK。 width や height の外でも描画できます。l (lineto) m 25,50 l 200,50 … e
l @3,45, @5,70,… e・ 現在のペン位置から (x, y) 座標で指定した位置まで
直線を引きます。
・ 指定はオートシェイプ内部の絶対座標です。
・ パラメータは "x, y座標値" のペアで連続で指定できます。c (curveto) m 0,0 c 0,50, 100,50,
100,0 x e
m 0,0 c @0,@1, @2,@3,
@4,@5 e・ 現在のペン位置から、制御点1, 制御点2, 終点 をそれぞれ
(x, y) 座標で指定し、ベジエ曲線を引きます。
・ 指定はオートシェイプ内部の絶対座標です。
・ パラメータは 6つずつ連続で指定できます。
※ ベジエ曲線の指定において、制御点は曲線が通過する点では
ありません。
たとえば、縦横 1:2 の長方形を想定し、長辺の端点に
開始点・終点 を置き、もう一方の長辺に 制御点1(開始点側)・
制御点2(終点側) を設定すると、ベジエ曲線はこの長方形領域を
目一杯に使った半円弧形状になります。
x (close) m 50,25 l 50,50, … x e ・ 現在のペン位置からサブパスの開始点(m や t で指定された点)
まで直線を引いて図形を閉じます。
・ 描画の開始点=終了点となり、新しいペン位置もこの閉じた点
(開始点=終了点)に移ります。
・ パラメータはありません。e (end) m … e m … e ・ サブパスを終了します。
・ パラメータはありません。t (rmoveto) m 0,0 … t 15,-4 … e ・ 新しいサブパス(一連の描画)の開始点を (cpx+x, cpy+y) 座標で
指定します。
・ 指定は現在のペン位置 (current pen x, current pen y) からの
相対座標です。
・ パラメータは "x , y 座標値" を示す 2つのみです。r (rlineto) r -10,50
r 20,-20, -5,10, …・ 現在のペン位置から (cpx+x, cpy+y) 座標で指定した場所まで
直線を引きます。
・ 指定は現在のペン位置 (current pen x, current pen y) からの
相対座標です。
・ パラメータは "x, y座標値" のペアを連続で指定できます。v (rcurveto) v 0,10, 10,0, 0,-10 ・ 現在のペン位置から、制御点1, 制御点2, 終点 をそれぞれ
(cpx+x, cpy+y) 座標で指定し、ベジエ曲線を引きます。
・ 指定は現在のペン位置 (current pen x, current pen y) からの
相対座標です。
制御点1 は前の命令結果からの相対座標、制御点2 は制御点1
からの相対座標、終点は制御点2 からの相対座標を指定します。
・ パラメータは 6つずつ連続で指定できます。nf (nofill) … e m … nf e … ・ e 命令で区切られたサブパス図形に関して、塗り潰し禁止
にします。
・ m や t で開始点を指定している場合は m(t)〜e 間で指定します。
※ 通常は e の直前で指定します。
・ 後述の fill 属性でオートシェイプ全体を "true" にしていても、
nf を記述したサブパスは塗り潰しが行われません。
・ パラメータはありません。ns (nostroke) … e m … ns e … ・ e 命令で区切られたサブパス図形に関して、線(輪郭線)描画を
禁止します。
・ m や t で開始点を指定している場合は m(t)〜e 間で指定します。
※ 通常は e の直前で指定します。
・ 図形中に領域の塗り潰しだけで形状を表現する箇所を作るために
使用します。
・ パラメータはありません。ae
(angleellipseto)ae 400,400, 60,40,
@3,@4・ 楕円弧を中心座標 (x, y), 半径長 (w, h), 開始角度, 終了角度を
指定して描画します。
その際、直前のペン位置から描画開始点まで直線が引かれます。
・ 中心は絶対座標。 半径長は横・縦方向のサイズ。
開始角度は x 軸の正方向を 0 とし、反時計周りを正とする
fd 単位の絶対的な角度方向。
終了角度は時計回りを正とした開始角度からの fd 単位の
相対角度(増分)。
・ パラメータは 6つずつ連続で指定できます。al (angleellipse) al 400,400, 60,40,
@3,@4・ ae と同様の命令ですが、直前のペン位置から描画開始点までの
直線は引かれません。at (arcto) at 100,20, 900,980,
@0,@1, @2,@3・ 楕円弧を、
* 楕円を内包する長方形領域を定義する x, y 座標 (x_left, y_top),
(x_right, y_bottom) の 4つのパラメータと
* 開始点角度・終了点角度を楕円の中心からの方向で示す
x, y 座標(半径方向ベクトル)の 4つのパラメータとで
描画します。
その際、直前のペン位置から描画開始点まで直線が引かれます。
・ 開始点から終了点まで、楕円(長方形範囲)の中心に対し、
反時計回りに描画されます。
・ パラメータはすべて絶対座標です。
・ パラメータは 8つずつ連続で指定できます。ar (arc) ar 100,20, 900,980,
@0,@1, @2,@3・ at と同様の命令ですが、直前のペン位置から描画開始点までの
直線は引かれません。wa
(clockwisearcto)wa 100,20, 900,980,
@0,@1, @2,@3・ at と同様の命令ですが、開始点から終了点まで、楕円(長方形
範囲)の中心に対し、時計回りに描画されます。wr
(clockwisearc)wr 100,20, 900,980,
@0,@1, @2,@3・ ar と同様の命令ですが、開始点から終了点まで、楕円(長方形
範囲)の中心に対し、時計回りに描画されます。qx
(elliptical
quadrantx)m 500,0 qx 1000,500 ・ 現在のペン位置から (x, y) 座標で指定した位置まで、
1/4 楕円(1長径-短径間)を、描画します。
・ 楕円弧の描き出しは x 軸に平行で、描画の終了は y 軸に平行。
・ パラメータは 2つずつ連続で指定できます。
※ qy と交互に使って円や楕円を作るのに便利です。
基本図形の「ドーナツ」もこれらの命令で作られてます。qy
(elliptical
quadranty)m 500,0
qx 1000,500
qy 500,1000・ 現在のペン位置から (x, y) 座標で指定した位置まで、
1/4 楕円(1長径-短径間)を、描画します。
・ 楕円弧の描き出しは y 軸に平行で、描画の終了は x 軸に平行。
・ パラメータは 2つずつ連続で指定できます。
※ qx と交互に使って円や楕円を作るのに便利です。
基本図形の「ドーナツ」もこれらの命令で作られてます。qb
(quadratic
bezier)m 0,0 l 100,0
qb 150,0, 150,50
l 150,150 e・ 制御点および終点を (x, y) 座標で指定し、1区間または連続で
2次ベジエ曲線区間を定義します。
・パラメータは制御点座標として 2つずつ連続 + 終点座標として 2つ
指定できます(2*n + 2)。
※ このコマンドは描画そのものではなく、あくまで定義のようです。
例えば、l 等 他の描画命令間に入れて、部分的にベジエ曲線で
つなぐ場合とかに使用できます。
qb 命令単独では、x 命令で閉じた図形にしないと描画されません 。- ※ 「ノギス」 の例の path の中のコマンドや、上記のコマンド表の "例" の欄の中に "@0" とか "@3" とか、 "@" 付きの数字(@n) が見られます。
- これは、詳しくは後ほど説明しますが、 formulas エレメントで作られる変数のようなモノで、'◆' ハンドル の移動位置によって変化する値です。
- 例えば、この「ノギス」の例では、ジョウの動く側全体の座標と、デプスを表す長方形の右側 2頂点の座標に "@" 付き数字(@n) を使ってます。
- ※ ノギスのコードの例では、図形本体の座標指定を主に絶対座標で行い、私のサイン "H Nori" 部分を相対座標で指定して描画しています。
(そもそも種明かし的な説明サイトで、サインなんて意味無いんですが…。 まあ、絶対座標と相対座標の違いの参考になれば幸いです。)- ※ fd (Fractional Degrees) は deg. (degrees ; 度 ; °) に 2の16乗 すなわち 65536 を乗じた値の角度単位です。
- 塗り潰す場合は fill を指定する必要はありません。(デフォルトで fill="true" なので。)
または "#000"〜"#fff" で色を指定します。
- 色名は "black", "silver", "gray", "white", "maroon", "red", "purple", "fuchsia", "green", "lime",
"olive", "yellow", "navy", "blue", "teal", "aqua" のいずれかで指定します。- fill="true" で、fillcolor を指定しない場合、塗り潰しの色は "#ffffff" すなわち "white" になります。
<v:f eqn="val #0"/>
<v:f eqn="val #1"/>
<v:f eqn="sum @0 0 35"/>
・
・
・
<v:f eqn="sum @0 1000 0"/>
<v:f eqn="sum @0 35 0"/>
<v:f eqn="sum @0 225 0"/>
</v:formulas>
v, p1, p2 は演算子(関数・コマンド)の引数(パラメータ)を順番に表してますが、演算子によって引数の数は違います。
| 演算子(関数)と 引数の書式 | 計算式(計算結果) または処理 | 説明 |
|---|---|---|
| val v | v | ・ ガイド値の宣言。 言わば、定数の変数化です。 ・ 複数の計算式で同じ定数を使用する場合、この式で一度 変数化(@n 化)し、各計算式でそれを指定しておくと、 設計変更時にこの行を変更するだけで済みます。 ・ 計算結果は厳密です。 |
| sum v p1 p2 | v + p1 - p2 | ・ 加減算を行います。 ・ 足し算・引き算どちらかのみの場合は、p1, p2 のいずれかに "0" を入れることになります。 ・ 計算結果は厳密です。 |
| prod v p1 p2 | v * p1 / p2 | ・ 乗除算を行います。 ・ 掛け算・割り算どちらかのみの場合は、p1, p2 のいずれかに "1" を入れることになります。 ・ 計算結果は丸められます(四捨五入だと思います)。 ※ W3C の VML ドキュメントでは "product" となってますが、 "prod" と記述してください。 |
| mid v p1 | (v + p1) / 2 | ・ 2数の平均値を計算します。 ・ 結果は 0側に丸められます。 |
| abs v | |v| | ・ 絶対値を返します。 ・ 例えば @3 が "-4" の場合、<v:f eqn="abs @3"/> の結果は "4" となります。 ・ 結果は厳密です。 |
| min v p1 | min (v, p1) | ・ 2数のうち、小さい方を選択します。 ・ 結果は厳密です。 |
| max v p1 | max (v, p1) | ・ 2数のうち、大きい方を選択します。 ・ 結果は厳密です。 |
| if v p1 p2 | if v>0 then p1 else p2 | ・ v が 0より大きければ p1、そうでなければ p2 を返します。 ・ 結果は厳密です。 |
| mod v p1 p2 | √(v^2 + p1^2 + p2^2) | ・ 3数の二乗和平方根(根二乗和)を計算します。 ・ 実用上は、パラメータのどれかを "1" にして、2次元平面での、 x, y 座標系 → r, θ 座標系(極座標) 変換において r(半径長) の計算に使うのが主だと思います。 (言い換えると、直角三角形で斜辺の長さを他の 2辺から 求める計算です。) ・ 計算結果は厳密ではありません。 |
| atan2 v p1 | arctan (p1 / v) | ・ 極座標形式の角度座標の計算。 mod とともに x, y 座標系 → r, θ 座標系(極座標)変換に使用します。 ・ 正の x 軸から、 原点 (0,0) と (x=v, y=p1) 点を通る直線までの 角度(fd単位 = deg * 2^16)を返します。 ・ 結果を θ とした場合、tanθ = p1/v 。 ・ 直角三角形で例えると、v, p1 を直角で接続した 2辺とした場合、 辺 v と斜辺との角度を計算します。 ・ 計算結果は厳密ではありません。 |
| cos v p1 | v * cos (p1) | ・ cos 値(x 成分)の計算。 ・半径 v, 角度 p1 (単位は fd = deg. * 2^16) のベクトルの x 成分 (cos 値)を返します。 ・ 直角三角形で例えると、斜辺(長さ v )と角度 p1 で接続している 辺の長さを計算します。 ・ 計算結果は厳密ではありません。 |
| sin v p1 | v * sin (p1) | ・ sin 値(y 成分)の計算。 ・ 半径 v, 角度 p1 (単位は fd = deg. * 2^16) のベクトルの y 成分 (sin 値)を返します。 ・ 直角三角形で例えると、斜辺(長さ v )と角度 p1 を成す角の 対辺の長さを計算します。 ・ 計算結果は厳密ではありません。 |
| cosatan2 v p1 p2 | v * cos (arctan (p2 / p1)) | ・ atan2 と cos の組み合わせ。 ・ 計算結果は厳密ではありませんが、内部の計算精度は完全。 ※ atan2 で算出した角度で cos の計算をするなら、 最初からこの演算子を使った方が良いということでしょうか? 計算式の数も減らせるし…。 |
| sinatan2 v p1 p2 | v * sin (arctan (p2 / p1)) | ・ atan2 と sin の組み合わせ。 ・ 計算結果は厳密ではありませんが、内部の計算精度は完全。 ※ atan2 で算出した角度で sin の計算をするなら、 最初からこの演算子を使った方が良いということでしょうか? 計算式の数も減らせるし…。 |
| sqrt v | √v | ・ 平方根の計算。 ・ 計算結果は正で、厳密ではありません(切り捨て)。 |
| sumangle v p1 p2 | v + p1* 2^16 - p2* 2^16 | ・ 角度の加減算。 ・ v は fd 単位(deg.* 2^16)で、p1 と p2 の単位は deg. 、 計算結果も fd単位(deg.* 2^16)です。 ・ 計算結果は厳密です。 |
| ellipse v p1 p2 | p2 * √(1 - (v/p1)^2) | ・ 楕円形状の計算。 ・ v を楕円の y 軸側の半径、p1 を x 軸側の半径とすると、 √(1 - (v/p1)^2) は離心率。 ・ 計算結果は厳密ではありません。 |
| tan v p1 | v * tan (p1) | ・ tan 値の計算。 ・ 半径 v, 角度 p1 (単位は fd = deg. * 2^16) のベクトルの y 成分 (sin 値)と x 成分 (cos 値)の比を返します。 ・ 直角三角形で例えると、斜辺(長さ v )と角度 p1 で接続している 辺の長さで残りの辺の長さを割った値を算出します。 ・ 計算結果は厳密ではありません。 |
| 値 | 例 | 説明 |
|---|---|---|
| @n | prod @3 4 1 | n+1番目(n+1行目)の計算式の結果。 最初の行の計算結果が @0 です。 引数として指定できるのはその計算式より前にある計算式の計算結果のみです。 |
| #n | sum #1 400 0 | '◆' ハンドルの座標の初期値として v:shape 内の adj で指定したパラメータを示し、 最初のパラメータを #0 として #7 まで引数として指定できます。 |
| width | sum @5 300 width | v:shape の codesize 属性で定義したオートシェイプの x 座標のサイズ(幅)。 |
| height | sum @5 300 height | v:shape の codesize 属性で定義したオートシェイプの y 座標のサイズ(高さ)。 |
| xcenter | sum xcenter @2 0 | オートシェイプ領域内中心の x 座標。 |
| ycenter | sum ycenter @2 0 | オートシェイプ領域内中心の y 座標。 |
属性 例 説明 position position="#0,#1" ・ '◆' ハンドルの位置を (x, y) 座標形式で指定します。
・ 通常、座標位置は '◆' ハンドルを手動で自由に動かすために
"#0"〜"#8" で指定します。
・ X,Y どちらかの方向の動きを禁じたり、別の '◆' ハンドル の挙動
によって位置を変えるときなど、場合に応じて、定数や "@n"などの
特殊引数を指定します。
※ 座標を固定する場合、 "center" という特殊パラメータを指定する
こともできます。polar polar="400,400"
polar="xcenter,ycenter"・ '◆' ハンドルの挙動を formulas において極座標形式
(r半径方向座標, θ角度方向座標) で扱うことを宣言し、
その原点 (r=0, θ=0) の位置を (x, y) 座標形式で指定します。invx invx="true" ・ '◆' ハンドルの X座標位置を formulas において
"原点のX座標 + X座標サイズ - X座標位置"
の値に変換して取り扱います。
・ polar を宣言している場合は r座標位置を
"r座標サイズ - r座標位置"
の値に変換して取り扱うと思いますが、未確認なのでわかりません。
・ デフォルト "false" なので、適用しない場合は、わざわざ
invx="false" と記述する必要はありません。invy invy="true" ・ '◆' ハンドルの Y座標位置を formulas において
"原点のY座標 + Y座標サイズ - Y座標位置"
の値に変換して取り扱います。
・ polar を宣言している場合は θ座標位置を
"360×2^16 [fd] - θ座標位置"
の値に変換して取り扱います。
・ デフォルト "false" なので、適用しない場合は、わざわざ
invy="false" と記述する必要はありません。xrange xrange="0,1000" ・ '◆' ハンドルの X座標の( polar を宣言してる場合は R座標の)
移動範囲を "最小値, 最大値" の形式で指定します。
・ 定数の他に"@n" などの特殊引数を指定できます。
・ 値を省略した場合、移動の範囲制限はありません。yrange yrange="0,1000" ・ '◆' ハンドルの Y座標の( polar を宣言してる場合は θ座標の)
移動範囲を "最小値, 最大値" の形式で指定します。
・ 定数の他に"@n" などの特殊引数を指定できます。
・ 値を省略した場合、移動の範囲制限はありません。radiusrange radiusrange="100,300" ・ polar を宣言してる場合に、'◆' ハンドルの R座標の移動範囲を
"最小値, 最大値" の形式で指定します。
・ 定数の他に"@n" などの特殊引数を指定できます。
・ 値を省略した場合、移動の範囲制限はありません。-
- 【2】 仮オートシェイプの作成
- FrontPage 2003 を立ち上げ、新規作成の状態で、デザインビュー(下部ウィンドウ)でツールバーの「オートシェイプ」から、 何でも良いので仮のオートシェイプを描きます。
- 独立メニューの 「四角形」や「オーバル」 を描くのが一番手っとり早いでしょう。
-
- すると、【0】項で説明した通り、デザインビューでは描いたオートシェイプが選択状態になり、コードビュー(上部ウィンドウ)では <body>〜</body> 内の <p>〜</p> 内にオートシェイプに対応する VML コードが記述され、選択状態になってます。
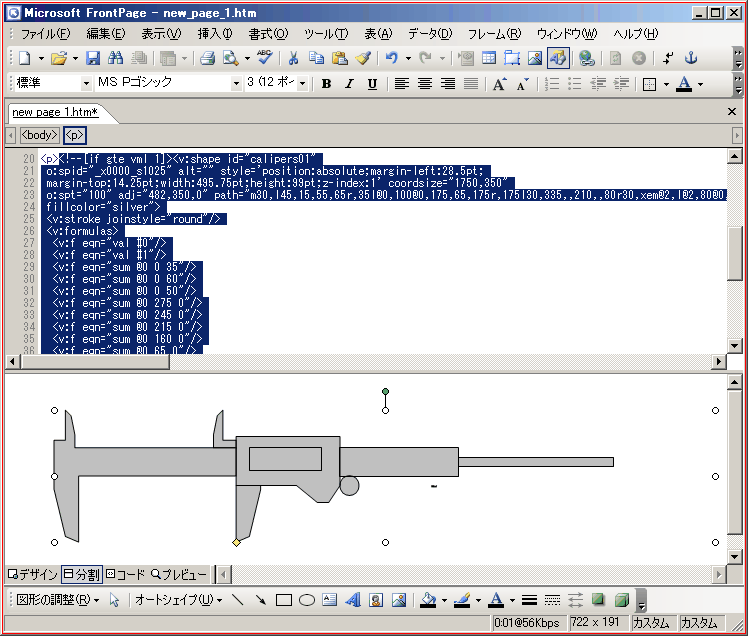
- 【3】 自作オートシェイプ VML コードの上書きと調整
- では、いよいよ【1】で作った自作オートシェイプを具現化します。
- 自作オートシェイプの VML コード(テキスト)をテキストエディタからコピーし、FrontPage 2003 のコードビュー(上部ウィンドウ)の <body>〜</body> 内の <p>〜</p> 内 (仮オートシェイプのVMLコード) に上書きで貼り付けます。
- 張り付けただけでは、デザインビュー(下部ウィンドウ)に反映されませんので、デザインビューのどこかをクリックします。
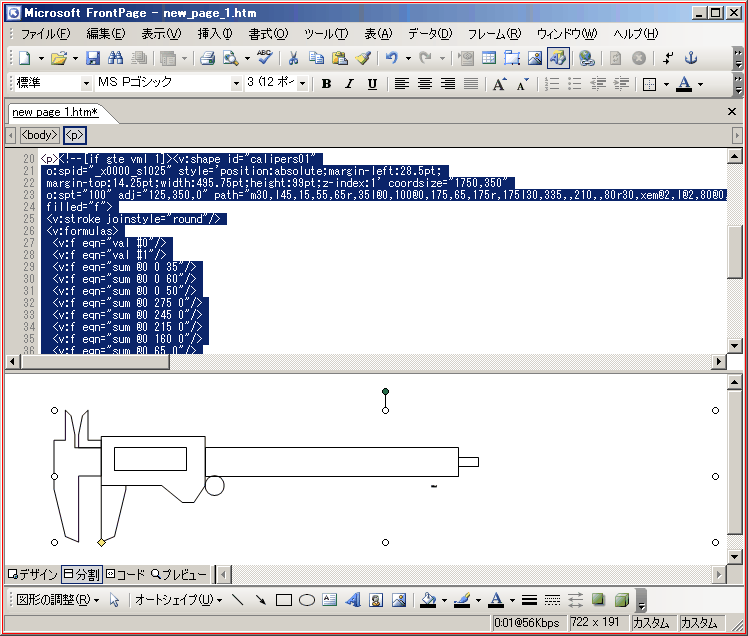
- すると、自作オートシェイプがデザインビューに具現化されます。
- さらに、オートシェイプをクリックすると以下のようにコードビュー・デザインビューとも選択状態になります。
- (この例では「塗り潰しなし」なので、輪郭線上をクリックします。)
- すると、【0】項で説明した通り、デザインビューでは描いたオートシェイプが選択状態になり、コードビュー(上部ウィンドウ)では <body>〜</body> 内の <p>〜</p> 内にオートシェイプに対応する VML コードが記述され、選択状態になってます。
-
- コードビューを見ると、FrontPage 2003 の最適化機能で多少書式や命令等が変更されているのがわかります。
- 例えば、mm 単位は pt 単位に変更されたり、 fill="false" は filled="f" になったりしています。
- でも、この辺のことはあまり気にしないで OK です。 重要なのはデザインビューのオートシェイプが思い通りの形になってるかどうかです。
- 形状が思い通りでなかった場合はもう一度元のテキストコードを見直します。
- 自作オートシェイプがデザインビューに正しく表示されましたら、 '◆' ハンドルを動かして動作を確認したり、 オートシェイプ自体を右クリックして 「オートシェイプの書式設定」 で、サイズ、塗り潰しやその色の設定、線の種類や太さなどを変更してみます。
- (このノギスのモデルは、塗り潰しが無いので輪郭線上を右クリックしましょう。)
- コードビューを見ると、FrontPage 2003 の最適化機能で多少書式や命令等が変更されているのがわかります。
-
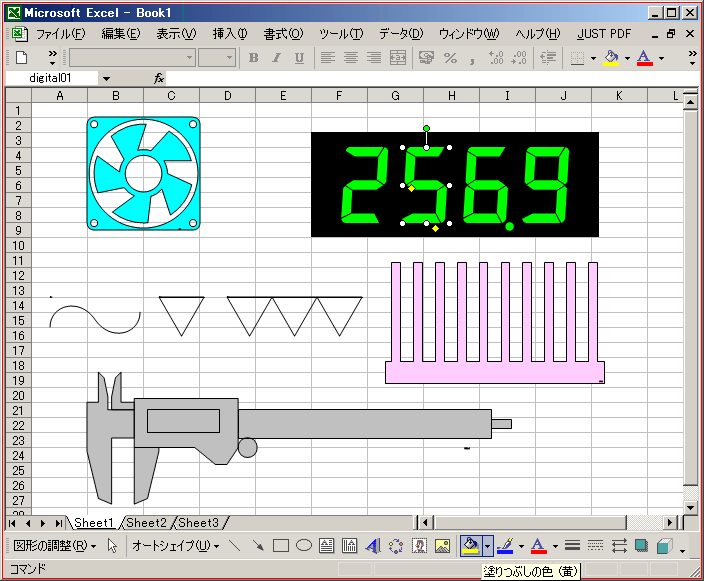
- 【4】 完成した自作オートシェイプの使用・保存
- FrontPage 2003 上でデザインが固まったらデザインビューのオートシェイプをコピーして、Excel/PowerPoint/Word の作成・更新画面に張り付けます。
- これで、Office 上で自由に使えるオリジナルオートシェイプ部品が完成したことになりますので、あとはストック専用のファイルを作って保存します。
-
- 以上で、終わりです。
ちょっとしたこと
- VMLで記述する段階でかなり細かい設定ができますが、オートシェイプにしてしまってからいくらでも変更できる
設定はしなくてもOKです。
- v:formulus の v:f eqn で 'prod' (乗除算) を誤って W3C の VML ドキュメントのコマンド表通りに 'product' と記述すると、
FrontPage にコピーしたときに何故か 'sum' (加減算) になってしまいます。
- v:shape の path における楕円弧や極座標系の命令や、v:formulus の f:eqn における演算子では、回転方向の正負や回転角(座標)の与え方がまちまちなので、
常に気をつけておきましょう。
たとえば、sin や cos などの三角関数演算子は、x 座標は右方向、y 座標は下方向が正なので、x 軸の正方向を 0 とした時計回りを正の角度と想定しますが、 path の ae コマンドなどは反時計回りが正の角度となります。 path の ae 命令はさらに、開始角度が絶対指定で、終了角度が開始角度からの相対座標なので 本当に気をつけないとドツボにハマリます。
- FrontPage 2003 のデザインビューで(通常の機能としての)オートシェイプを作成すると、コードビューにその VML コードが自動生成されますが、
これがオリジナルオートシェイプを設計する際に大いに参考になります。
v:shape の path の曲線・極座標系命令の使い方とか、 v:shapetype の使い方や、オートシェイプ内にテキスト入力領域を設定する方法とかがわかります。
- FrontPage 2003 に VML コードその他をコピーしたとき、数値の表現や単位が FrontPage にとって都合のよい形式に変更されます。
"fill" が "filled" という表記になったり、未指定の属性( <v:stroke joinstyle="round"/> など)が設定されたり、 「0」 (ゼロ)や 「 , 」 (区切り記号) などが省略されたり、 オートシェイプ位置なども 「 mm 」 単位が 「 pt 」 単位に変換されます。
path 内の記述も区切り記号や空白・改行が省略され、人間にとってはかなりツライ表記になります。
よって、変更やデバッグの際は、FrontPage 側ではなく、元のテキストエディタ側を変更してコピーした方が賢明です。
- おもな参考 Web サイト, etc.
- 【1】 Interactive Web Graphics with VML: Parameterized Shapes in FrontPage By Oleg Kobchenko 元ネタです。 英語が苦でなければ、ココを見ていただければ私のこのページは不要です。
- 【2】 Vector Markup Language (VML) W3C の VML ドキュメント。
- 【3】 ベクトルマークアップ言語(VML) どら猫本舗さんによる 【2】の和訳。 【2】とともに大変参考になりました。
- 【4】 msdn Vector Markup Language (VML) Microsoft の VML リファレンス。
- 【5】 ベクトルタイム 色々と参考にさせていただきました。
- 【6】 VMLについて かなり詳細な考察をされてます。 大変勉強になりました。
- 【その他】 Yahoo! GROUPS "sliderule (The International Slide Rule Group)"
趣味の一つが「計算尺」なので、このメーリングリストに入ってます。 すべてはここからはじまりました。
- ● メッセージ No.28073 (Andrew Nikitin)
「計算尺ダイアグラムのオートシェイプを作成した」 というメッセージ。 これを読んで自作オートシェイプ部品に興味を持ちました。
- ● メッセージ No.28078 (Andrew Nikitin) 「作成の際 【1】 を参考にした」 というリンク付きメッセージ。 ただし、すでにリンク先が変更されていて、【1】を探すのにちょっと手間取りました。
- ● nsg-sr1.doc (Andrew Nikitin) 「計算尺ダイアグラムのオートシェイプ」 が張り付けられた Word 文書。 これを見て、滑尺とカーソルが自由に動かせることに感動し、自分でも作ってみようと思いました。
※ このファイルはグループ(ML)に登録し、ログイン(サインイン)してないとダウンロードできないと思います。
※ それにしても、Andrew Nikitin さんってすごい!!! この方は オンラインで計算尺を設計できるサイト も開設しています。 - ● メッセージ No.28078 (Andrew Nikitin) 「作成の際 【1】 を参考にした」 というリンク付きメッセージ。 ただし、すでにリンク先が変更されていて、【1】を探すのにちょっと手間取りました。
- このサイトは常に工事中のようなものです。
- norihito4の「秘密基地」
- 施工者 : norihito4(お笑いエンジニア)
- norihito4の「秘密基地」
- 改版メモ
- 2015/09/18 : 内容変更・削除,公開
- 2009/10/xx : 初版(非公開)
