K尺なしで立方根

　昔のマンハイム計算尺【 A [ B, (CI), C ] D // [ S, L, T ] 】には K尺がありません。

　この計算尺で立方根（3乗根）を計算する方法を紹介します。

　もちろん L尺があるので、常用対数を利用した一般の巾乗・乗根計算を行う方法でも良いのですが、表面の対数尺度のみで計算可能です。

　紹介する手法はいずれも　a = x^3 = x * x^2　の計算操作を利用し、計算尺上で x = a^(1/3) を探します (a>0, x>0) 。

※ K尺を使った立方根計算

　各手法の紹介の前に、まず、K尺による立方根計算の原数の設定方法について知ってなければなりません。

　通常、立方根（3乗根）は K[a]→D[a^(1/3)] で得ますが、K尺には 3つの領域（K1,K2,K3）があり、原数 a の数値の頭が小数点から何桁目にあるかで、設定領域が異なります。

K1領域(0～10)：　頭の桁が 1,4,7,・・・桁目の数値を設定。 1.23, 1230, 0.00123 等。

K2領域(10～100)：　頭の桁が 2,5,8,・・・桁目の数値を設定。 12.3, 12300, 0.0123 等。

K3領域(100～1000)：　頭の桁が 3,6,9,・・・桁目の数値を設定。 123, 123000, 0.123 等。

　原数を小数点から 3桁ずつ区切っていき、数値の頭部分の桁数を数えると考えやすいです。

　　1|234 ,　0.|001|234　等、数値の頭部分が 1桁なら K1領域,

　 12|340 ,　0.|012|34　等、2桁なら K2領域,

　123|400 ,　0.|123|4　　等、3桁なら K3領域に設定します。

Ⅰ． sl[i]>D[x] h>B[x] → A[x^3] から x を逆算

　

　CI尺が無い場合のオーソドックス（死語）な手法です。

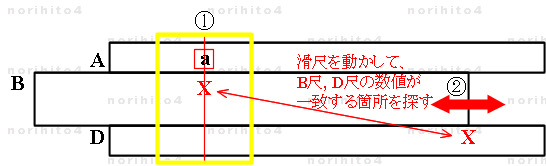
　　　h>A[a] find(x1,x2|x1=x2)【 B[x1]>h ⇔ sl[i]>D[x2] 】　→　B[a^(1/3)] ，D[a^(1/3)]

【1】 h>A[a]　：　①: 　立方根をとる数値（原数） a を A尺にとり、カーソル線を合わせます。; 　; ※ 原数 a を設定する領域にご注意願います。本来 K尺で K1(1～10), K3(100～1000) 領域に設定する数値（1.23, 123, 0.00123 等）を A1領域(1～10) に設定し、 K2領域(10～100) に設定する数値（12.3, 1230, 0.0123 等）を A2領域(10～100)に設定します。; 　
【2】 find(x1,x2|x1=x2)【 B[x1]>h ⇔ sl[i]>D[x2] 】　：　②: 　滑尺を操作して、カーソル線下の B尺の数値(x1) と、滑尺基線に対する D尺の数値(x2) が一致する(x1=x2) 箇所を探します。; 　
【3】 → B[a^(1/3)] ，D[a^(1/3)]　：　②: 　B尺と D尺で一致した数値が a の立方根 a^(1/3) です。;

Ⅱ． A[x] CI[x] → A[x^3] から x を逆算

　

　CI尺がある場合は、A尺とCI尺だけで求められます。

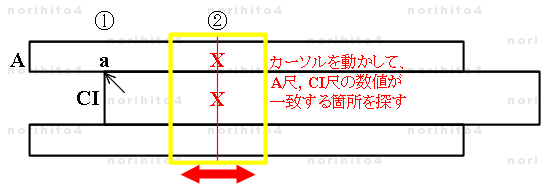
　　　sl[i]>A[a] find(x1,x2|x1=x2)【 h>A[x1] ⇔ h>CI[x2] 】　→　A[a^(1/3)] ，CI[a^(1/3)]

【1】 sl[i]>A[a]　：　①: 　立方根をとる数値（原数） a を A尺にとり、滑尺の基線を合わせます。; 　; ※ 原数 a を設定する領域にご注意願います。本来 K尺で K1(1～10), K3(100～1000) 領域に設定する数値を A1領域(1～10) に設定し、K2領域(10～100) に設定する数値を A2領域(10～100)に設定します。; 　
【2】 find(x1,x2|x1=x2)【 h>A[x1] ⇔ h>CI[x2] 】　：　②: 　カーソルを操作して、A尺の数値(x1) と CI尺の数値(x2) が一致する(x1=x2) 箇所を探します。; 　
【3】 →　A[a^(1/3)] ，CI[a^(1/3)]　：　②: 　A尺と CI尺で一致した数値が a の立方根 a^(1/3) です。;

※ Ⅰの方法では、カーソル線下と滑尺基線上との遠い2箇所を見比べて解を探さなければなりませんでしたが、この方法では、カーソル線下の 2尺度を見比べるのでかなり楽に解が探せます。

Ⅲ．倒尺法

　

　CI尺がない計算尺でも Ⅱと同様の操作を行えるよう、滑尺を上下逆にして挿入し、C尺を CI尺に見立てます。

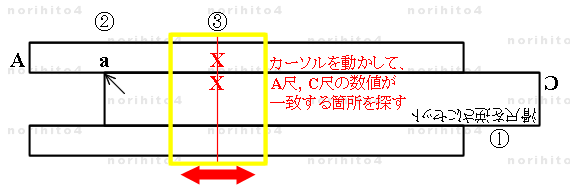
　　　逆sl[i]>A[a] find(x1,x2|x1=x2)【 h>A[x1] ⇔ h>逆C[x2] 】　→　A[a^(1/3)] ，逆C[a^(1/3)]

【1】逆sl[i]>A[a]　：　① ，②: 　まず、滑尺を上下逆にして挿入します（①）。そして、立方根をとる数値（原数） a を A尺にとり、滑尺の基線を合わせます（②）。; 　; ※ 原数 a を設定する領域にご注意願います。本来 K尺で K1(1～10), K3(100～1000) 領域に設定する数値を A1領域(1～10) に設定し、K2領域(10～100) に設定する数値を A2領域(10～100)に設定します。; 　
【2】 find(x1,x2|x1=x2)【 h>A[x1] ⇔ h>逆C[x2] 】　：　③: 　カーソルを操作して、A尺の数値(x1) と C尺の数値(x2) が一致する(x1=x2) 箇所を探します。; 　
【3】 →　A[a^(1/3)] ，逆C[a^(1/3)]　：　③: 　A尺と C尺で一致した数値が a の立方根 a^(1/3) です。;

※ この方法は、C尺が逆さとはいえ A尺と隣り合っており、さらに、同じカーソル線下で探すので、わりと楽です。

Ⅳ．ピックウォース法（分尺法）

　

　この手法はまず、計算尺に手を加える必要があります。 C尺に、その長さを 3等分するゲージライン（刻線）を 2つ刻まなければなりません。

　すなわち、 2.154 （=10^(1/3)）と 4.642 （=100^(1/3)）であり、K尺におけるの 10 と 100 のラインです。

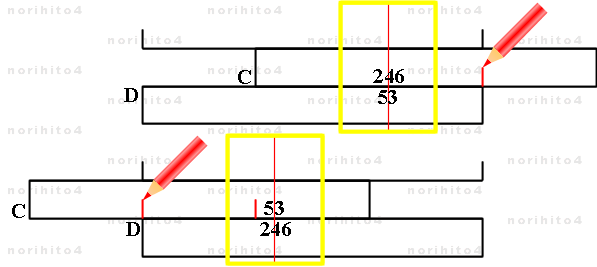
　このゲージラインは目で C尺の目盛を読んで直接引くことも可能ですが、 5.3/0.246 = 2.154, 2.46/0.53 = 4.642 が近いので、 C, D尺に 53 と 246 を交互にとって中合わせ法（滑尺法）で計算し、D尺基線上の C尺に線を引くと簡単です。

　では、本番です。基本的な操作はⅠの方法と同じです。

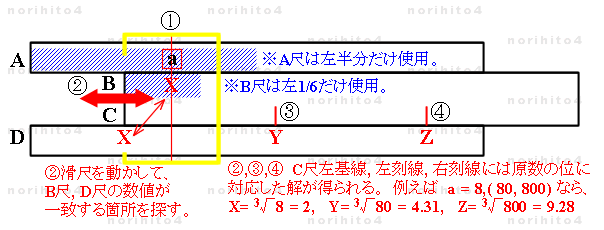
　　　h>A[a] find(x1,x2|x1=x2)【 B[x1]>h ⇔ sl[l.i]>D[x2] 】

　　　　　　　　→　B[a^(1/3)]@h ，D[a^(1/3)]@sl[l.i] ，D[a^(1/3)]@C[2.154] ，D[a^(1/3)]@C[4.642]

【1】 h>A[a]　：　①: 　立方根をとる数値（原数） a を A尺の左側の領域（A1領域）にとり、カーソル線を合わせます。; 　; ※ 本手法では、原数 a の桁に依らず A尺は左半分しか使用しません。; 　
【2】 find(x1,x2|x1=x2)【 B[x1]>h ⇔ sl[i]>D[x2] 】　：　②: 　滑尺を操作して、カーソル線下の B尺の数値(x1) と、滑尺基線に対する D尺の数値(x2) が一致する(x1=x2) 箇所を探します。; 　; ※ 本手法では、B尺は左半分の領域のさらに左 1/3 の領域、すなわち左 1/6 の領域しか使用しません。; 　
【3】 →　B[a^(1/3)]@h ，D[a^(1/3)]@sl[l.i] ，D[a^(1/3)]@C[2.154] ，D[a^(1/3)]@C[4.642]　：　②: 　B尺と D尺で一致した数値が、K尺なら K1領域に設定する a の立方根 a^(1/3) です。; 　また、C尺に引いた左右 2本のゲージラインに対応する D尺の数値も、それぞれ K2, K3領域の a の立方根 a^(1/3) です。;

※ 本手法では、他の方法よりも解を探す範囲が狭く、基線の置き換えも発生しません。

※ ヘンミ No.30 や 32 の C尺にゲージラインを入れてみてはどうでしょう。