「計算尺愛好会」分室　『計算尺の秘密基地』 => テクニック編 =>

加減算!?

　まず最初に断っておきますが、そもそも計算尺は乗除形式の計算を簡便に行うために作られた計算器なので、 加減算は他の方法で行うのが本筋です（「計算尺詳解」（宮崎治助）では、「邪道であるとみなして良い」と・・・）。

　いくつか紹介しますが、やはり、あまり実用的ではありません。 紙と鉛筆を使った方がはるかに速くて正確です。

　

　

�T． 滑尺 L尺とカーソルを使う

　

　最も本質的で基本的な手法です。 滑尺に配備された L尺とカーソルで、加算を基線法（カーソル法）, 減算を中合わせ法（滑尺法） で固定尺にスタックしていきます。 最後に L尺でカーソル線下の値を読み取ります。

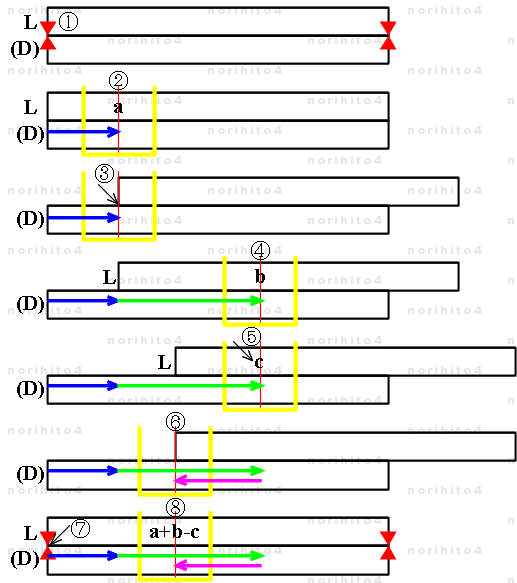
　以下に a + b - c の場合の手順を示します。

　

　 　

　

　sl[i]>st[i] h>L[a] sl[i]>h h>L[b] L[c]>h h>sl[i] sl[i]>st[i]　→　L[ a+b-c ]

　

【1】　�@： まず、片面尺で L尺が滑尺裏面にある場合は滑尺を引き抜いて裏返し、L尺側を表にして固定尺にセットします。

【2】　sl[i] > st[i]　： �@： 固定尺と滑尺をピッタリ合わせます。

【3】　h > L[a]　： �A： カーソル線を L尺 a に合わせます。（固定尺に a 加算）

【4】　sl[i] > h　： �B： 滑尺基線をカーソル線に合わせます。

【5】　h > L[b]　： �C： カーソル線を L尺 b に合わせます。（固定尺に b 加算）

【6】　L[c] > h　： �D： L尺 c をカーソル線に合わせます。

【7】　h > sl[i]　： �E： カーソル線を滑尺基線に合わせます。（固定尺に c 減算）

【8】　sl[i] > st[i]　：　固定尺と滑尺をピッタリ合わせます。（固定尺上の結果を L尺で読む準備）

【9】　→　L[d]　：　カーソル線下の L尺の数値 a+b-c を読み取ります。

　

　※注意1： L尺が逆目盛の場合でも、方向が逆になるだけでやることは同じです。

　※注意2： 通常の対数尺上の乗除算と違い、各項の位取りをきちんと合わせなければなりません。

　例えば、123+45+67+89 の場合、123 の百の位の "1" は別にし、計算尺では 23+45+67+89 で計算するような形態にします。

　つまり、各項の数の大きさにあまり大きな隔たりが無い場合にしか使えません。

　※注意3： 基線の置き換えが発生する場合は・・・？

　計算尺での計算とは別に考えている上の桁の数値を＋1, −1 します。

　L尺をサイクリックに永遠につながっているものとしてイメージしてください。 1回転で上の桁が＋1, −1されます。

　

　

�U． a + b = a * ( 1 + b/a) と考える

　

　結構いろんな教科書に載ってる手法です。 加減算を下式右辺のように変形します。

　

　a ± b = a * (1 ± b/a) ・・・・・・・・・・・・(1)

　

　これを「加減式の乗法表現」と言うそうです。 もちろん b を外に出した形　b * (a/b ± 1)　にもできます。

　項数が増えても同様に順にくくっていきます。 以下に 4項の足し算の場合の例を示します。

　

　a + b + c + d = a * 〔 1 + b/a * { 1 + c/b * ( 1 + d/c ) } 〕・・・・(2)

　

　ここでは式(1) について説明します。

（式(2) のように多項の場合も括弧の内側の方から順に同様のことを繰返しやれば良いからです。）

　

　計算尺の操作手順は以下の通りです。

　

　

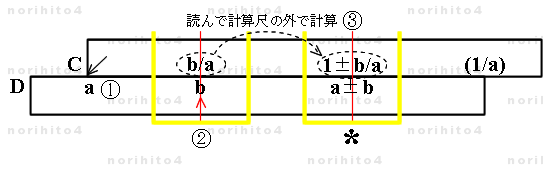
【1】 C[i]>D[a] h>D[b] → C[b/a]　：　�@, �A

　D尺 a に C尺基線を合わせ（C尺：D尺 = 1：a の関係）、カーソル線を D尺 b に合わせると C尺に b/a が得られます。

　C尺と D尺の関係（C尺：D尺 = 1：a ）はそのままにしておきます。

　

【2】 C尺に得た b/a から 1±b/a を、計算尺の外（頭の中や筆算）で計算します。

　

【3】 《C[i]=D[a]》 h>C[1±b/a] → D[a±b]　：　�B

　C尺と D尺の関係（C尺：D尺 = 1：a ）を保ったまま、カーソル線を C尺の 1±b/a に合わせると、 D尺に a±b を得ることができます。

　

　C尺と D尺の立場を逆にしてもOKです（C尺 a をD尺基線に合わせ、最終的に a+b を C尺に得る）。

　

　この手法を利用すると以下のような計算も可能です。

　

　

◆ a^2 ± b^2 ， √(a^2 ± b^2)

　

　a^2 ± b^2 = a^2 * (1± b^2/a^2)　，　√(a^2 ± b^2) = a * √(1± b^2/a^2)

　

　　　として、計算します。

　

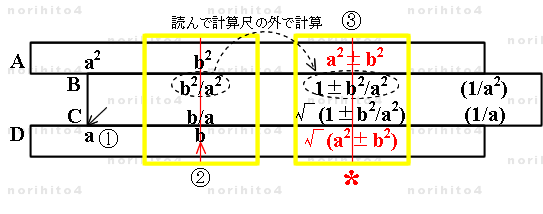
【1】 C[i]>D[a] h>D[b] → B[b^2/a^2]　：　�@, �A

　D尺 a に C尺基線を合わせ（C尺：D尺 = 1：a の関係）、カーソル線を D尺 b に合わせると B尺に b^2/a^2 が得られます。

　C尺と D尺の関係（C尺：D尺 = 1：a ）はそのままにしておきます。

　

【2】 B尺に得た b^2/a^2 から 1± b^2/a^2 を、計算尺の外（頭の中や筆算）で計算します。

　

【3】 《C[i]=D[a]》 h>B[1± b^2/a^2] → A[a^2±b^2] ，D[√(a^2±b^2)]　：　�B

　C尺と D尺の関係（C尺：D尺 = 1：a ）を保ったまま、カーソル線を B尺の 1±b^2/a^2 に合わせると、 A尺に a^2±b^2 を得ることができ、同時に D尺には √(a^2±b^2) を得ることができます。

　

　

◆ 1/a ± 1/b

　

　1/a ± 1/b = 1/a * (1± a/b)

　

　　　として、計算します。

　

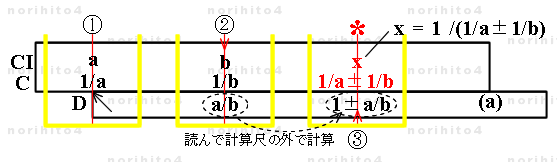
【1】 h>D[i] CI[a]>h h>CI[b] → D[a/b]　：　�@, �A

　カーソルを使ってCI尺 a を D尺基線に合わせ（D尺 = a / CI尺 ，C尺：D尺 = 1：a の関係）、 カーソル線を CI尺 b に合わせると D尺に a/b が得られます。

　固定尺と滑尺の関係（C尺：D尺 = 1：a ）はそのままにしておきます。

　

【2】 D尺に得た a/b から 1± a/b を、計算尺の外（頭の中や筆算）で計算します。

　

【3】 《st[i]=CI[a]》 h>D[1± a/b] → C[1/a±1/b] ，CI[ 1/(1/a±1/b) ]　：　�B

　固定尺と滑尺の関係（C尺：D尺 = 1：a ）を保ったまま、カーソル線を D尺の 1±a/b に合わせると、 C尺に 1/a±1/b を得ることができます。

　また、同時に、CI尺には 1/(1/a±1/b) を得ることができ、並列抵抗や直列コンデンサの合成値の計算にも使用できます。

　

※ DI尺のある計算尺では、C, D, DI尺を使っても同様のことができます。

　

　

◆ 1/a^2 ± 1/b^2

　

　1/a^2 ± 1/b^2 = 1/a^2 * (1± a^2/b^2)

　

　　　として、計算します。

　

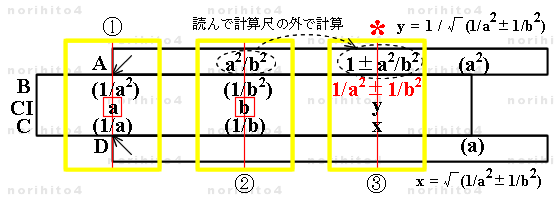
【1】 h>st[i] CI[a]>h h>CI[b] → A[a^2/b^2]　：　�@, �A

　カーソルを使ってCI尺 a を固定尺（A尺, D尺）の基線に合わせます。

　次に、カーソル線を CI尺 b に合わせると A尺に a^2/b^2 が得られます。

　固定尺と滑尺の関係（C尺：D尺 = 1：a ，B尺：A尺 = 1：a^2）はそのままにしておきます。

　

【2】 A尺に得た a^2/b^2 から 1± a^2/b^2 を、計算尺の外（頭の中や筆算）で計算します。

　

【3】《st[i]=CI[a]》 h>A[1±a^2/b^2]

　　　　 → B[1/a^2±1/b^2] ，C[√(1/a^2±1/b^2)] ，CI[1/√(1/a^2±1/b^2)]　：　�B

　固定尺と滑尺の関係（C尺：D尺 = 1：a ）を保ったまま、カーソル線を A尺の 1±a^2/b^2 に合わせると、 B尺に 1/a^2±1/b^2 を得ることができます。

　また、同時に、C尺には √(1/a^2±1/b^2) ，CI尺には 1/√(1/a^2±1/b^2) が得られます。

　

　いずれの方法も頭の中で、1を足したり、1から引いたりしなければなりません。 「計算尺で加減算をやった」感はいま一つです。

　

　

�V． 三角関数尺度を使う

　

　直角三角形を解く三平方の定理を利用して a±b の計算をします。

　

◆ a+b

　

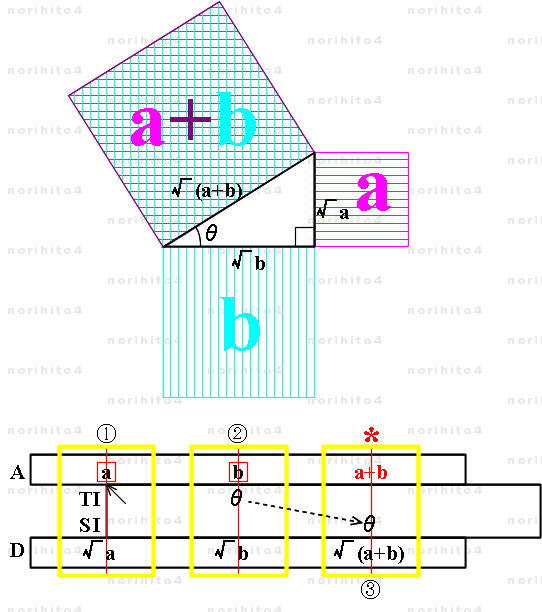
　直角三角形の斜辺を一辺とした正方形の面積は、他の 2辺をそれぞれ一辺とした正方形の面積の和と同じです（三平方の定理）。

　a>0 , b>0 とし、 √a と √b を直角三角形の直角を作る辺の長さとして計算します。

　

　

　

　

※ 直角三角形に強い、逆目盛の三角関数尺度 SI, TI で説明します。 滑尺は三角関数尺度のある面を前面にしてセットしておきます。

　

　【1】 h>A[a] TI[i]>h h>A[b] → TI[θ]　：　�@, �A

　A尺 a に TI尺の基線を合わせた後、カーソル線を A尺 b に合わせ、TI尺上に角度θを得ます。

　固定尺と滑尺の位置関係はそのままにしておきます。

　

　【2】《sl[i]=A[a]》 h>SI[θ] → A[a+b]　：　�B

　固定尺と滑尺の位置を保ったまま、カーソル線を SI尺の θに合わせ、A尺に a+b を得ます。

　

※ リーツ（リッツ）式等、 S, T尺配備の計算尺の場合は滑尺の天地を逆にして台尺に差し込み、逆目盛尺と同様に操作します。

　

　【1】 h>A[a] 逆T[i]>h h>A[b] → 逆T[θ]

　【2】《sl[i]=A[a]》 h>逆S[θ] → A[a+b]

　

※ 旧マンハイム式（S尺が A尺 , T尺が D尺に対応）の場合は、滑尺の天地逆に加え、 S尺にθをとった後、 さらに基線とθ間の距離を加えなければなりません。

　

　【1】 h>A[a] 逆T[i]>h h>A[b] → 逆T[θ]

　【2】《sl[i]=A[a]》 h>逆S[θ] 逆S[i]>h h>逆S[θ] → A[a+b]

　

◆ a-b

　

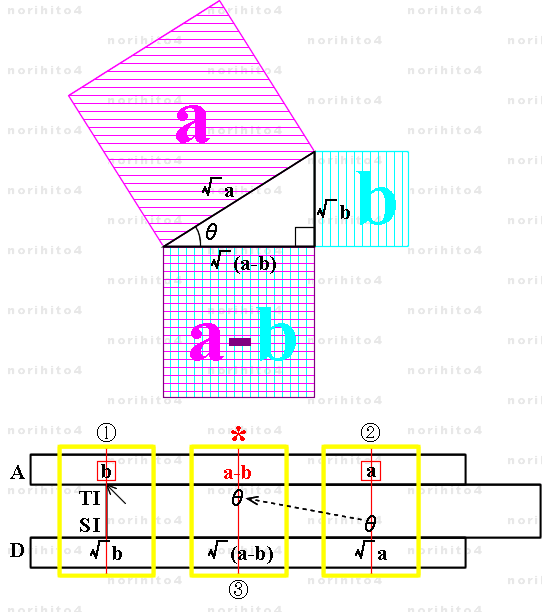
　考え方は a+b の場合と同じですが、a>0 , b>0 で √a を既知の斜辺、他方の既知の一辺を √b として、 正方形の面積の差（ (√a)^2 - (√b)^2 = a-b ）を計算します。

　

　

　

※ 直角三角形に強い、逆目盛の三角関数尺度 SI, TI で説明します。 滑尺は三角関数尺度のある面を前面にしてセットしておきます。

　

　【1】 h>A[b] TI[i]>h h>A[b] → TI[θ]　：　�@ ，�A

　A尺 b に TI尺の基線を合わせた後、カーソル線を A尺 a に合わせ、SI尺上に角度 θ を得ます。

　固定尺と滑尺の位置関係はそのままにしておきます。

　

　【2】《sl[i]=A[b]》 ( 6°< θ < 45°)　h>TI[θ] → A[a-b] ，

( 45°< θ < 84°，TI2あり )　h>sl[i] sl[i]>h h>TI2[θ] → A[a-b] ，

( 45°< θ < 84°，TI2なし )　h>sl[i] TI[90-θ]>h h>sl[i] → A[a-b]　：　�B

　

　6°< θ < 45°の場合（ a-b > b ）は固定尺と滑尺の位置を保ったまま、カーソル線を TI尺の θに合わせ、A尺に a-b を得ます。

　45°< θ < 84°の場合（ a-b < b ）は滑尺操作が必要です。

　TI2尺がある場合は、基線の置き換えの後、TI2尺の θ にカーソル線を合わせて A尺に a-b を得ます。

　TI2尺がない場合は、滑尺基線にカーソル線を合わせた後、滑尺操作で TI尺の 90-θ （=赤θ） を カーソル線まで移動し、最後にカーソル線を滑尺基線に合わせると、A尺に a-b が得られます。

　

※ リーツ（リッツ）式等、 S, T尺配備の計算尺の場合は滑尺の天地を逆にして台尺に差し込み、 逆目盛尺と同様に操作します。 （操作記述は略します）

　

　【1】 h>A[b] 逆T[i]>h h>A[b] → 逆T[θ]

　【2】《逆sl[i]=A[b]》 ( 6°< θ < 45°)　h>TI[θ] → A[a-b] ，

( 45°< θ < 84°，T2あり )　h>逆sl[i] 逆sl[i]>h h>逆T2[θ] → A[a-b] ，

( 45°< θ < 84°，T2なし )　h>逆sl[i] 逆T[90-θ]>h h>逆sl[i] → A[a-b]

　

※ 旧マンハイム式（S尺が A尺 , T尺が D尺に対応）は、滑尺の天地逆に加え、 S尺に θ を得る際、 A尺 の b と a の距離を 1/2 にしなければなりませんが、幸い、旧マンハイム式は滑尺に L尺がありますので、 L尺で測って S尺 基線から A尺 b ，a の距離の 1/2 にある θ を得ます。

　L尺は右から左へ 0 〜 1 の LI尺とし、それが天地逆なので、左から右へ 0 〜 1 の L尺と同じになります。 （ヘンミ 40RK を想定してます。）

　

　【1】 h>A[b] 逆sl[i]>h h>A[a] → 逆LI[log(√a/√b)]

　【2】 計算尺 ，暗算 ，筆算などで、【1】で得た数値を 1/2 する。

　【3】 《逆sl[i]=A[b]》 h>逆LI[log(√a/√b)/2] → 逆S[θ]

　【4】 《逆sl[i]=A[b]》 ( 6°< θ < 45°)　h>逆T[θ] → A[a-b] ，

( 45°< θ < 84°)　h>逆sl[i] 逆T[90-θ]>h h>逆sl[i] → A[a-b]

　

　

---