『計算尺の秘密基地』 => テクニック編 =>

精密計算・精密読取り

　

【1】 精密読取その1

　

　実例にて、その方法を示します。

　

例： 9.7 ／ 6.75 (真値 1.43703703…)

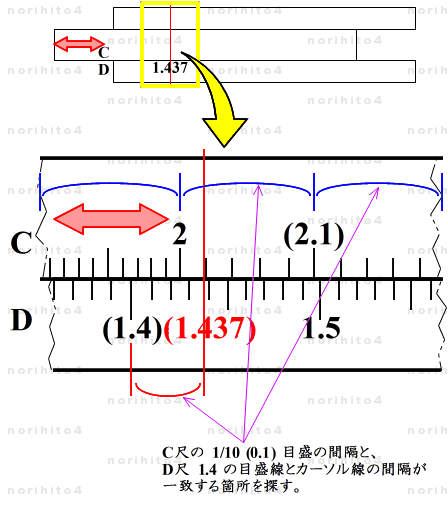
　D尺 9.7 に C尺 6.75 を合せると滑尺基線下のD尺に1.437 が得られます。

　h>D[9.7] C[6.75]>h → D[1.437]@sl[idx].

　

　

　解の位置にカーソル線を移動します。

　ここで、滑尺を移動し、C尺の 1/10 (0.1) 目盛の間隔と、D尺 1.4 の目盛線とカーソル線の間隔が一致する箇所を探します。

　探してゆくと、この場合、3.8 と 3.9 の目盛間隔が合致します。

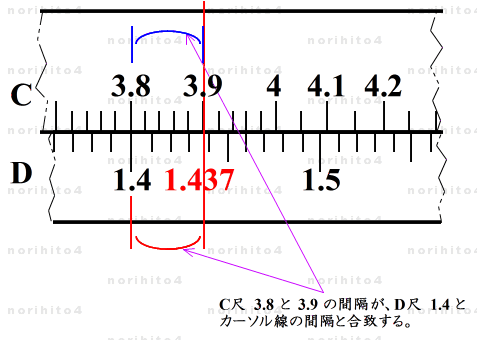
　このとき、滑尺基線に対する D尺に 369 が読め、これが 1.4 に続く小数となります。

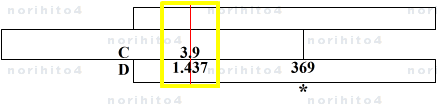
　よって、答えは 1.4369 となります。

　この例では真値と 0.0001 程度の誤差なので十分ですが、場合によっては、もっとズレたり、区間を決めかねたりします。

　とても 「1 桁多く読める」 とまでは言えませんが、例えば、「答えが 3.48 か 3.49 か微妙」 といった時にどちらか判断するときなどに使えます。

　

　

【2】 精密な数値設定

　

　尺度に数値を設定する場合も読み取りと同様の手段が使えます。

　実例にて、その方法を示します。

　

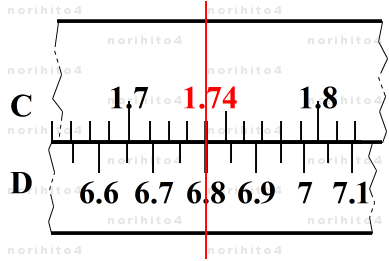
例： 6.8391 を D尺に設定する。

　まず、滑尺の左基線を D尺の 391 に合せ、次に D尺 6.8 にカーソル線を合せます。

　 次に、カーソル線に一番近い C尺の 1/100 (0.01) 目盛に着目し、滑尺を動かしてこの目盛（1.74 の目盛線）をカーソル線に合せます。

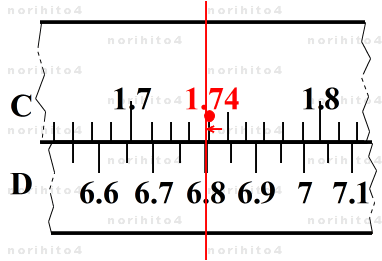
　最後に、1.74 の右隣 1/100 (0.01) 目盛である 1.75 に着目し、これにカーソル線を合せます。

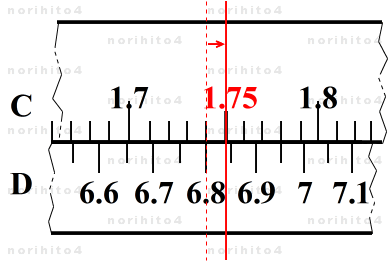
　これで、完了です。この例では、運良くほぼ 6.8391 にセットできたはずです。

　この方法では、最初に着目する目盛がカーソル線に近ければ近いほど精度よく数値を設定することができます。

　逆に言うと、カーソル線が C尺目盛間のど真ん中を通っていたらちょっとつらいです。

　

　

【3】 精密読取その2

　

　D尺上の数値 A を精密に読み取るとします。

　

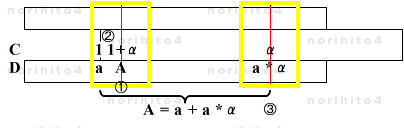
�@まず、A にカーソル線を合せます。

�A次に、C尺の基線を A に最も近い目盛線 a に合せ、カーソル線下 C尺の値を 1 + α としますと、

A = a * (1 + α) = a + a *α

　と表すことができます。　

�Bよって、カーソル線を C尺の α に合せると、その線下の D尺に a *αが得られ、A は a と a +α の和として比較的精密に読むことができます。

　

例： 3.37*0.735　（真値 2.47695）

　h>D[3.37] C[0.735]>h → D[2.475]@sl[idx]

　

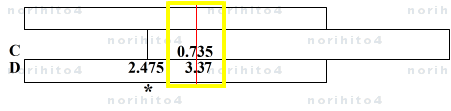
　カーソル線を滑尺基線（ D尺答え）に合せ、滑尺の基線を D尺 2.4 の目盛線に合せます。

　カーソル線下のC尺を読むと 1.032 なので 1 を引いて、 C尺 0.032 に対する D尺を読むと 0.0768 が得られます。

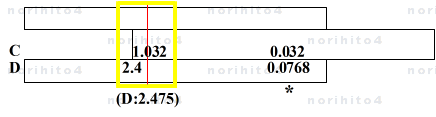
2.4（目盛） + 0.0768 = 2.4768

　どうやら、そこそこの精度は得られそうです。でも、この方法は精度が体調でかなり左右されそうな気がします。

　

　

【4】 精密読取その3

　

　D尺上の数値 A を以下の手順で精密に読み取ります。

　

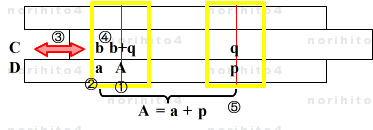
�@まず、D尺 A にカーソル線を合せます。

�A次に、その左側で近い目盛線 a を選び、A = a + p とします。

�B滑尺を移動してゆき、C尺において、D尺の a（目盛） と A（カーソル線） の幅に合う目盛のペアを探します。

�C合致した目盛のペアをそれぞれ、b と b + q とします。

�D比例関係により、

b / a = (b+q) / A = (b+q) / (a+p)

　

b / a = (b+q) / (a+p) = q / p

　が成立しますので、C尺上の q に対する D尺上に p の値を見いだすことができ、A = a + p として Aの値を読み取ることができます。

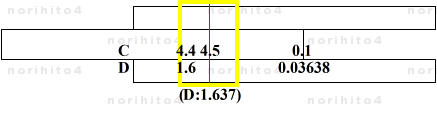
例： 9.1 ／ 5.56　（真値 1.6366906…）

　

　まず、割り算を行います。

h>D[9.1] C[5.56]>h → D[1.637]@sl[idx]

　

　滑尺基線にカーソルを移動し、D尺にてカーソル線（解）に近い目盛として 1.6 の目盛線を選びます。

　次に、滑尺を動かして、D尺の 1.6 目盛線とカーソル線の成す幅にあう、目盛のペアをC尺から探します。

　1.75 と 1.79 の目盛線が該当し、その差 0.04 （C尺） に対するD尺の値 0.03658 を読み取ります。

　よって、答えは、1.6 + 0.03658 = 1.6358 となります。

　合致する目盛線のペアは他にも 2.64 と 2.7 などいろいろありますが、4.4, 4.5 の 1/10 目盛のペアを選ぶと、【1】項の精密読取その1 と全く同じになります。

　また、【3】項の精密読取その2 も目盛ペアの代わりに基線と一般の数値を利用したもので、結局は本手法の変形と言えます。

　

　以上、計算尺をバーニヤとして使う方法でしたが、「ちょっとつらい」というのが率直な感想です。

　結局のところ、バーニヤで読み取る前に、目盛やカーソルがちゃんとした計算尺で計算の操作を神経質なくらい注意深く行わなければ何の意味もないし、うまく行っても劇的に精度が上がる訳でもないようで、素直に 50cm の計算尺を使った方が良いような気もします。

　

　

【5】 分割計算法

　

【5-1】 乗法の分割計算法

　

　乗数または被定数のどちらか一方の数を分割して二つの乗法形式の和として求めます。

　

例： 1.56 * 3.78 (真値 5.8968)

　

　計算尺で普通に計算すると、

h>D[1.56] CI[3.78]>h → D[5.90]@sl[idx].

　

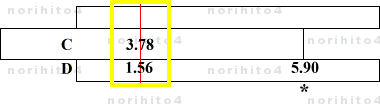
　答えは 5.90 ですが、分割計算すると、

1.56 * 3.78 = 1.56 * (3.00 + 0.78)

　 1.56 * 3.00 = 4.68　　　h>D[1.56] C[3.00]>h → D[4.68]

＋1.56 * 0.78 = 1.216　　h>D[1.56] C[0.78]>h → D[1.216]

──────────

　　　　　　　　　　5.896

　となり、かなり真値に近い値（相対誤差0.016%）になります。

　また、バーニヤ法を併用するとさらに精度が得られます。

　

　

【5-2】 除法の分割計算法

　

　除法の分割計算は正直面倒です。

　被除数を A, 除数を B とし、被除数 A は B の a 倍と b 倍との和であるとしますと、

A / B = a + b

A = B・a + B・b

A - B・a = B・b

∴ b = (A - B・a) / B

　まず、a をキリの良い目盛線の値として探索・設定し、次に残りの b を得ることになります。

　

例： 9.1 ／ 5.56　（真値 1.6366906…）

　

　まず、計算尺で割り算を行います。

h>D[9.1] C[5.56]>h → D[1.637]@sl[idx]

　

　a は商の有効数字の 1桁目をとります。すなわち、a = 1 。

　これより、

B・a = 5.56 * 1 = 5.56

　

B・b = A - B・a = 9.1 - 5.56 = 3.54

　

b = 3.54 / B = 3.54 / 5.56 = 0.637 ???

h>D[3.54] C[5.56]>h → D[0.637 ???]@sl[idx]

　

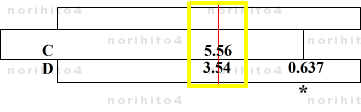
　あれっ？ これだと A / B = a + b = 1 + 0.637 = 1.637 で、普通に割り算したのと変わりないですね…。

　ということで、a は商の有効数字の 2桁目までをとり、比較的キリの良い目盛線の値をとることにします。

　とりあえず、a = 1.5 としてみます。

　これにより、

B・a = 5.56 * 1.5 = 8.34

h>D[5.56] CI[1.5]>h → D[8.34]@sl[idx]

　

B・b = A - B・a = 9.1 - 8.34 = 0.76

　

b = 0.76 / B = 0.76 / 5.56 = 0.1367

h>D[0.76] C[5.56]>h → 0.1367

　

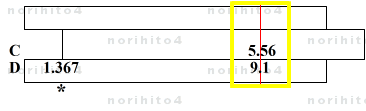
∴ A / B = a + b = 1.5 + 0.1367 = 1.6367

　ということで、真値に対して 0.02 % 程度の誤差となりました。

　商の最初の 1 桁の数字が 1 の時は、有効数字の 2桁目まで見て a を設定しないとダメみたいですね。

　

　

【6】 宮崎治助の精密計算法

　

　本来この方法は「測微カーソル」という特殊なカーソルを使うと効率よく計算できるそうですが、通常の計算尺で計算するのは少し面倒なようです。

　数値を、計算尺上の目盛の数値（有効数字 1〜2 桁）を母数として、残りの微細な数値を母数で除した値で表します。

　今、A という数が与えられたとします。母数を a, 微細部分を α= (A - a) / a で表しますと、Aは

A = a (1 +α)

と、表すことができます。

　例えば、A = 4567 としますと、

A = 4567 = 4500 * (1 + a)

　

a = (4567 - 4500) / 4500 = 67 / 4500

h>D[67] C[4500]>h → D[0.01489]@sl[idx]

　

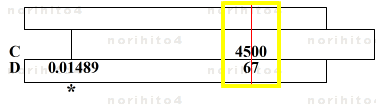
a = 67 / 4500 = 0.01489

　よって、

4567 = 4500 * (1 + 0.01489)

と、表現することができます。

　

　

【6-1】 乗法

　

　A * B において、

A = a (1 +α)

　

B = b (1 +β)

とすれば、

A * B = a b * (1 +α) * (1 +β)

　

　　　　= a b * (1 +α+β+αβ)

　ここで、 αβ<< 1 とし、無視できるものとしますと、

A * B ≒ a b (1 + α+β)

　よって、積も個々の数と同様の形状となり、母数の積を母数とし、微細部分の和の割合を求めれば良いことになります。

　

例： 2.376 * 4.155　（真値 9.868125）

　

　普通に計算尺で計算しますと、

h>D[2.376?] CI[4.155]>h → D[9.87]

　

　次に、本手法を使ってみます。

2.376 = 2.3 * (1 +α)

α= (2.379-2.3) / 2.3 = 0.079 / 2.3

h>D[0.076] C[2.3]>h → D[0.0330]@sl[idx]

　

α= 0.076 / 2.3 = 0.0330

　

∴ 2.37 = 2.3 * (1 + 0.0330)

　

4.155 = 4.1 * (1 +β)

　

β= (4.155 - 4.1) / 4.1 = 0.055 / 4.1

h>D[0.055] C[4.1]>h → D[0.01341]@sl[idx]

　

β= 0.055 / 4.1 = 0.01341

　

∴ 4.155 = 4.1 * (1+ 0.01341)

　

2.376 * 4.155 ≒ 2.3 * 4.1 * (1 + 0.0330 + 0.01341)

　　　　　　　　　≒ 2.3 * 4.1 * (1 + 0.04641)

　h>D[2.3] CI[4.1]>h → D[9.43]@sl[idx]

　

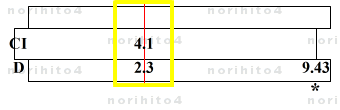
　　　　　　　　　≒ 9.43 * (1 + 0.04641)

　　　　　　　　　≒ 9.43 + 9.43 * 0.04641

h>D[9.43] CI[0.0464] → D[0.437]

　

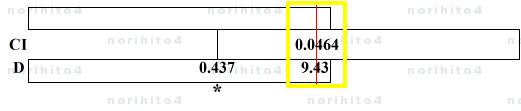
　　　　　　　　　≒ 9.43 + 0.437

　　　　　　　　　≒ 9.867

　

【6-2】 除法

　

　A / B において、

A = a (1 +α)

B = b (1 +β)

とすれば、

A / B = (a / b) * { (1 +α) / (1 +β) }

　　　　= (a / b) * [ { (1 +α) * (1 -β) } / { (1 +β) * (1 -β) }

　　　　= (a / b) * { (1 +α-β-αβ) / (1 -β²) }

　ここで、 αβ<< 1, β2<< 1 で、無視できるとしますと、

　　　　≒ (a / b) (1 + α-β)

　よって、商も個々の数と同様の形状となり、母数の積を母数とし、微細部分の和の割合を求めれば良いことになります。

　

例： 5.126 / 2.319　（真値 2.21043553…）

　

　普通に計算尺で計算しますと、

h>D[5.126?] C[2.319?]>h → D[2.21?]

　

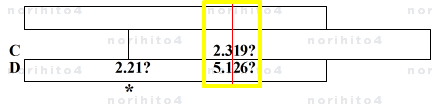
　次に、本手法を使ってみます。

5.126 = 5.1 * (1 +α)

　

α= (5.126 - 5.1) / 5.1 = 0.026 / 5.1

h>D[0.026] C[5.1]>h → D[0.00510]@sl[idx]

　

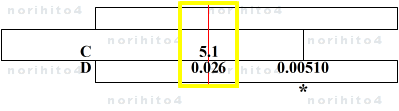
α= 0.026 / 5.1 = 0.00510

　

∴ 5.126 = 5.1 * (1+ 0.00510)

　

2.319 = 2.3 * (1 +β)

　

β= (2.319 - 2.3) / 2.3 = 0.019 / 2.3

h>D[0.019] C[2.3]>h → D[0.00826]@sl[idx]

　

β= 0.019 / 2.3 = 0.00826

　

∴ 2.319 = 2.3 * (1 + 0.00826)

　

5.126 / 2.319 ≒ (5.1 / 2.3) * (1 + 0.00510 - 0.00826)

　　　　　　　　　≒ (5.1 / 2.3) * (1 - 0.00316)

h>D[5.1] C[2.3]>h → D[2.22]@sl[idx]

　

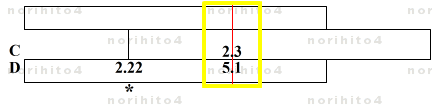
　　　　　　　　　≒ 2.22 * (1 - 0.00316)

　　　　　　　　　≒ 2.22 - 2.22 * 0.00316

h>D[2.22] CI[0.00316] → D[0.00702]

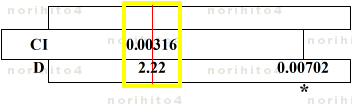
　　　　　　　　　≒ 2.22 - 0.00702

　　　　　　　　　≒ 2.21298

　乗法に比べてあまりぱっとしません。何が原因でしょう？

　

　

【7】 5桁と1桁の乗法

　

　5桁やそれ以下の数に、変化する 1桁の数を掛けることは、表計算等でよくあったそうです。

　表計算といっても、Excel ではなく、パソコンが現れる以前に、集計用紙に手書きで行っていたものです。

　身近なものでいえば、麻雀の点数記録用紙のイメージでしょうか。

　

　5桁の数に 1桁の数を乗じますと計算結果は 5〜6 桁になります。

　この計算結果を 5桁まで精密に読み取ることを計算尺を 2本使って行います。

　

例： 被乗数 48527,　乗数 6,　48527 * 6 （真値 291162）

　

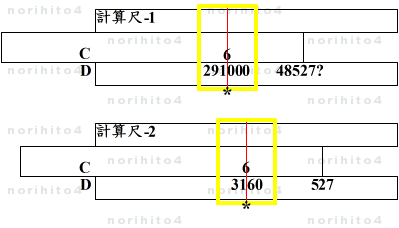
�@計算尺-1 の D尺に、被乗数をできるだけ精密に設定して滑尺の基線を合せます。

�A計算尺-2 の D尺に、被乗数の最後の3桁、この場合 527 を設定して滑尺の基線を合せます。

�B計算尺-1, 2とも、カーソル線を C尺の乗数 6 に合せて、対応する D尺の数値を読みます。

計算尺-1: h>D[48527?] sl[idx]>h h>C[6] → D[291000]@h

計算尺-2: h>D[527] sl[idx]>h h>C[6] → D[3160]@h

　

�C2つの計算尺操作の結果を組み合わせて解とします。計算尺-2の結果の最初の1桁 3 は計算尺-1の結果に含まれますので、削除します。

　

　よって、答えは 291000 + 160 = 291160 となり、真値に非常に近い値になります。

　

　この方法は乗数が 2, 3, 4, 5, … と変化する場合には、カーソル移動だけで済みますので、非常に効率的です。

　

　逆に、乗数がただ一つの場合は、計算尺は 1本で十分であり、以下のような手順で可能です。

　上と同じ例を使用します。

　

�@D尺の 6（乗数）にC尺の右基線を合せます。

�Aカーソル線を C尺 48527 に合せて D尺に最初の3桁 291 を得ます。

�B同様にカーソル線を C尺 527 に合せて D尺に 3160 を得て、最初の 1桁 3 を捨てます。

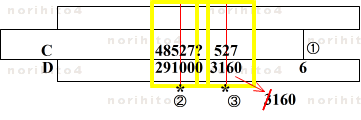
�C2つの結果を合成して、最終的な答え 291000 + 160 = 291160 を得ます。

　

さらに、精密に計算するには、カーソル線を C尺上の最後の 2桁 27 に合せ、対応する D尺に 162 を得て、最初の 2桁を捨てて、他の計算結果と合成します。

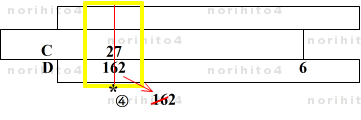
　答えは 291000 + 160 + 2 =291162 となり、真値を得ることができました。

　

　

【8】 平野式開平法

　

　5〜6 桁の平方根の計算に有力な方法です。

　

�@まず、A 尺, D 尺等で a の平方根 √a を計算します。

�A√a の最初の1桁〜2桁に近くてキリの良い数値（整数など） b を作り、c = a - b2 を筆算で計算します。

�Bさらに δ= c / (2・b) を計算尺で計算します。

�C近似的に √a ≒ b + δ なので、これを筆算で計算します。

　

例： √63.4　（真値7.96241169…）

　�@　　　　　√a = √63.4

h>A[63.4] → D[7.96]@h

　

√63.4 = 7.96 ≒ 8

　�A　　　　　b = 8,　c = a - b2 = 63.4 - 64 = - 0.6

　

　�B　　　　　δ= c / (2・b) = - 0.6 / 16

h>D[0.6] C[16]>h → D[0.0375]@sl[idx]

　

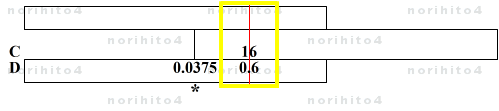
δ= - 0.6 / 16 = - 0.0375

　�C　　　　　√63.4 = b + δ= 8 - 0.0375 = 7.9625

　

　

　

改版メモ

・2015/05/04 ： 初版