二次方程式を解く
-
- 1変数の二次方程式を計算尺で解きます。
- 解法に適した計算尺は HEMMI P253 や HEMMI 2662 などです。
-
- ■二次方程式の解法
-
- 二次方程式の一般形は
- A x2 + B x + C = 0
- これを、両辺をAで割って以下の形に変更します。
- x2 + b x + c = 0 ‥‥‥‥‥ (1)
- または、
- x2 + 2 b' x + c = 0 ‥‥‥‥‥ (1)'
- 式(1), (1)' の係数・定数 a, b(b'), c の符号や大きさの関係で x の根の種類が変わってきます。
-
- ・根α, βと係数の関係
- ( x - α) ( x - β) = 0 ・・・・ (2)
-
- αβ= c ‥‥‥‥‥ (3), α+β= - b ‥‥‥‥‥ (4)
- ・根の判別
- ┃
- ┣━ c < 0 : 符号の異なる2実根 ‥‥‥‥‥ 【1】
- ┃
- ┗━ c > 0 ━┳━ b2 > 4 c : 同じ符号の2実根 ‥‥‥‥‥ 【2】
- ┃
- ┗━ b2 > 4 c : 虚根 ‥‥‥‥‥ 【3】
-
-
- 【1】 符号の異なる2実根 : c < 0
-
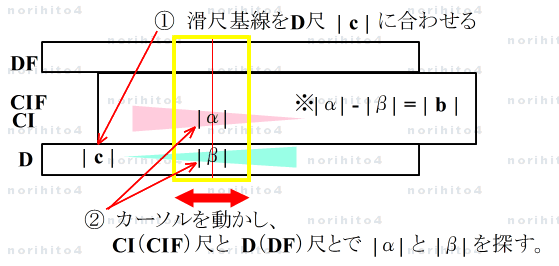
- 掛けて | c | となり、差が | b | となる 2数 |α|, |β| を計算尺上で探します。
- |αβ| = | c | , |α| - |β| = | b | ( |α| > |β| , αの符号は b と逆).
- 【1-1】 カーソルを動かして根の探索(D(DF)尺, CI(CIF)尺利用)
-
- ① D尺の | c | に滑尺の基線を合わせ、
- ② カーソルを動かして CI(CIF)尺とD(DF)尺とで、差が | b | となる、根 |α| と |β|を探します。
-
-
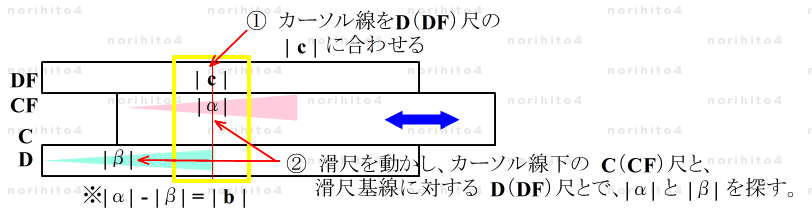
- 【1-2】 滑尺を動かして根の探索(D(DF)尺, C(CF)尺利用)
-
- ① D尺(DF尺)の | c | にカーソル線を合わせ、
- ② 滑尺を動かして、カーソル線下のC尺(CF尺)と滑尺基線に対するD尺(DF)尺とで、差が | b | となる、根 |α| と |β| を探します。
-
-
- 【2】 同符号の2実根 : c > 0 , b2 > 4c , b'2 > c
-
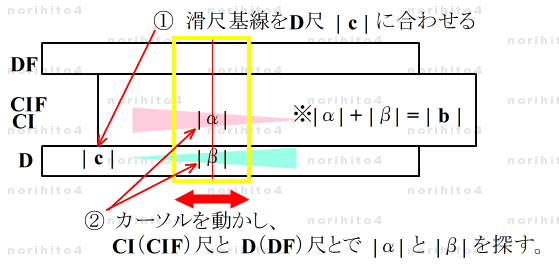
- 掛けて | c | となり、和が | b | となる 2数 |α|, |β| を計算尺上で探します。
- |αβ| = | c | , |α| + |β| = | b | (α, βの符号は b と逆).
-
- 【2-1】 カーソルを動かして根の探索(D(DF)尺, CI(CIF)尺利用)
-
- ① D尺の | c | に滑尺の基線を合わせ、
- ② カーソルを動かして CI(CIF)尺と D(DF)尺とで、和が | b | となる、|根 |α| と |β| を探します。
-
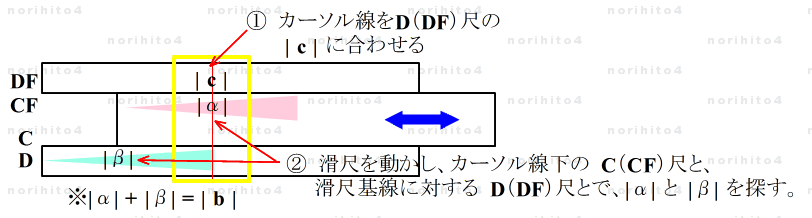
- 【2-2】 滑尺を動かして根の探索(D(DF)尺, C(CF)尺利用)
-
- ① D尺(DF尺)の | c | にカーソル線を合わせ、
- ② 滑尺を動かして、カーソル線下のC尺(CF尺)と滑尺基線に対するD尺(DF)尺とで、和が | b | となる、根 |α| と |β| を探します。
-
-
- 【3】 虚根 : c > 0 , b2 < 4c , b'2 < c
-
- 方程式を式(1)'の形に変形します。
- x2 + 2 b' x + c = 0 ‥‥‥‥‥ (1)'
- 虚根の形態は
- x = -b' ±√(c - b'2) ・i
- √(c - b'2) の部分をピタゴラスの定理を利用して計算します。(実根 x = -b' ±√(b'2 - c) の場合も使えます。)
-
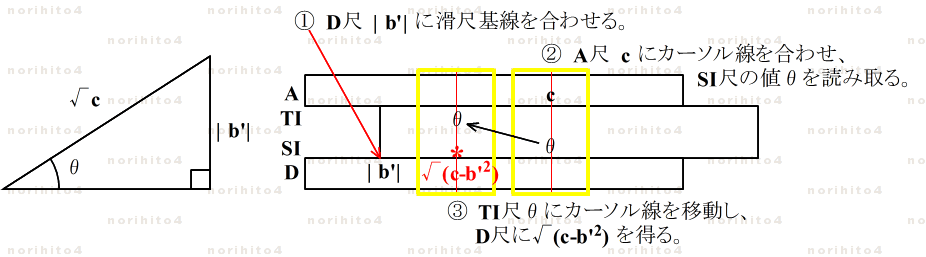
- A尺のある面に SI, TI 尺が来るように滑尺をセットしておきます。
-
- 三角関数尺度が S, T 尺の場合は滑尺を逆さにセットして SI, TI 尺とします。
-
- ① D尺 b' に滑尺の基線を合わせます。
- ② A尺 c にカーソル線を合わせて SI尺の値θを読み取ります。
- ③ TI尺 θにカーソル線をあわせて D尺上に √(c - b'2) を得ます。
-
- ※別解 (三角関数尺度を使用しない方法)
-
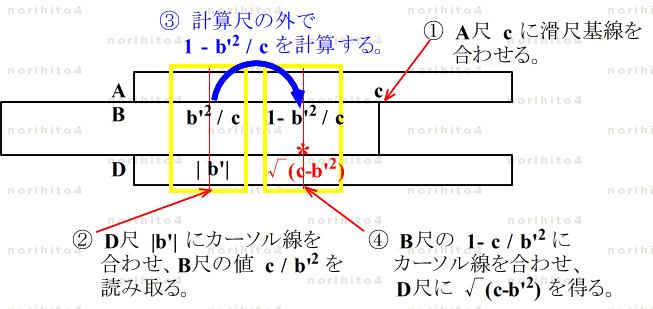
- A, B, D尺を使って √(c - b'2) の部分を計算します。(テクニック編「加減算!?」参照)
-
- ① A尺 c に滑尺の基線を合わせます。
- ② D尺 | b'| にカーソル線を合わせて B尺の値 c / b'2 を読み取ります。
- ③ 計算尺の外(暗算・筆算)で 1- c / b'2 を計算します。
- ④ B尺 1- c / b'2 にカーソル線をあわせて D尺上に √(c - b'2) を得ます。
-
-
- ■例題
-
- (1) 3.75 x2 + 5.30 x - 7.50 = 0
-
- (2) 2.33 x2 + 5.82 x + 2.45 = 0
-
- (3) 1.76 x2 + 3.67 x + 12.73 = 0
-
-
- ■解答
-
- (1) 3.75 x2 + 5.30 x - 7.50 = 0
-
- Ax2 + B x + C = 0 の形を x2 + bx + c = 0 の形に変形します。
-

- よって、式は以下のように表せます。
- x2 + 1.413 x - 2.00 = 0 , b = 1.413 , c = - 2.00
- c < 0 より、根は異符号の 2実根なので、解法【1】を用います。
-
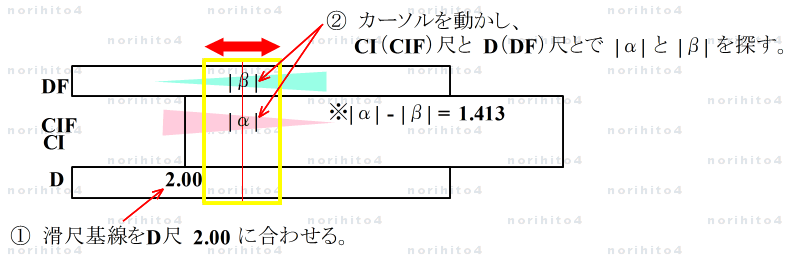
- 計算尺上である程度の検討をつけたら、| b | = |α| - |β| = 1.413 を目指して、より細かく探査します。
- EXCELでいうところの「ゴールシーク」です。
-
| 試行#
| |αm|
| |βm|
| |bm|=
|αm|-|βm|
|
|
| CIF尺
| DF尺
| 筆算
|
| 01
| 2.30
| 0.869
| 1.431
|
| 02
| 2.24
| 0.893
| 1.347
|
| 03
| 2.27
| 0.882
| 1.388
|
| 04
| 2.29
| 0.874
| 1.416
|
| 05
| 2.28
| 0.877
| 1.401
|
- #04 の |bm| 値が | b | = 1.413 に最も近いので、#04 の |αm|, |βm| を |α|, |β| として採用します。
- |α| = 2.29 , |β| = 0.874
- 大きい方が b の符号と逆となるので、
- α = -2.29 , β = 0.874
- よって、解は
- x = -2.29 , 0.874 (真値: x = -2.2876 , 0.8743)
-
- (2) 2.33 x2 + 5.82 x + 2.45 = 0
-
- (1) と同様に、Ax2 + B x + C = 0 の形を x2 + bx + c = 0 の形に変形しますと、以下のように表せます。
- x2 + 2.50 x + 1.052 = 0 , b = 2.50 , b2 = 625 , c = 1.052 , 4c = 4.21
- c > 0 , b2 > 4c より、根は同符号の 2実根なので、解法【2】を用います。
- 足して 2.5 、掛けて 約 1 であることから、 αm = 2 , βm = 0.5 ぐらいをイメージして探査を開始してみます。
-
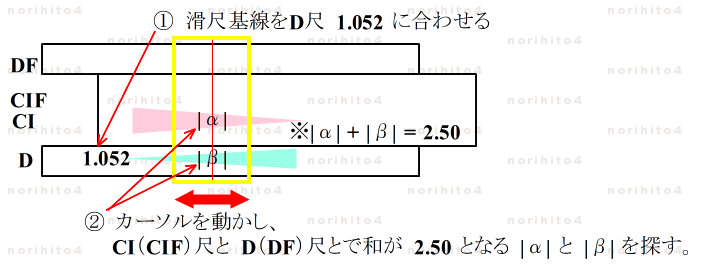
- (1) と同様に、| b | = |α| + |β| = 2.50 を目指して、探査します。
-
| 試行#
| |αm|
| |βm|
| |bm|=
|αm|+|βm|
|
|
| CIF尺
| DF尺
| 筆算
|
| 01
| 2.02
| 0.515
| 2.535
|
| 02
| 1.930
| 0.545
| 2.475
|
| 03
| 1.970
| 0.5335
| 2.5035
|
| 04
| 1.960
| 0.5365
| 2.4965
|
| 05
| 1.965
| 0.535
| 2.500
|
- #05 の |bm| 値が | b | = 1.413 に最も近いので、#04 の |αm|, |βm| を |α|, |β| として採用します。
- |α| = 1.965 , |β| = 0.535
- b の符号と逆なので、
- α = -1.965 , β = -0.535
- よって、解は
- x = -1.965 , -0.535 (真値: x = -1.9619 , -0.5360)
-
- (3) 1.76 x2 + 3.67 x + 12.73 = 0
-
- (1) , (2) と同様に、Ax2 + B x + C = 0 の形を x2 + bx + c = 0 の形に変形しますと、以下のように表せます。
- x2 + 2.085 x + 7.23 = 0 , b = 2.085 , b2 = 4.35 , c = 7.23 , 4c = 28.9
- c > 0 , b2 < 4c より、根は複素数となりますので、解法【3】を用います。
- x2 + 2b'x + c = 0 の形に変形します。
- x22 + 2*1.043 x + 7.23 = 0 , b' = 1.043 , c = 7.23
-
- x = -b' ±√(c - b'2) ・i = -1.043 ±√(7.23 - 1.0432) ・i
- √(c - b'2) = √(7.23 - 1.0432) の部分をピタゴラスの定理を利用して計算します。
-
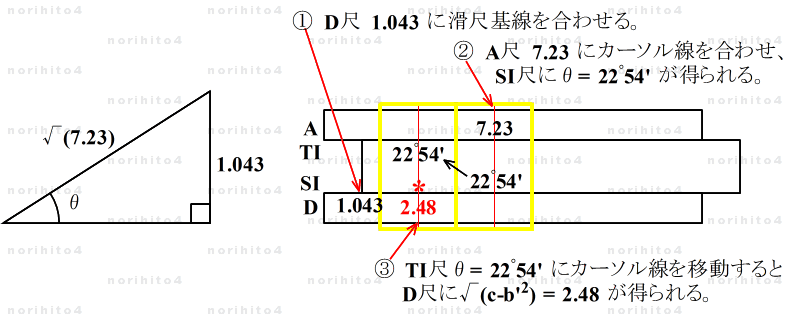
- よって、
- x = -b' ±√(c - b'2) ・i = -1.043 ±√(7.23 - 1.0432) ・i = -1.043 ±2.48 i
- あらためて、解は、
- x = -1.043 ±2.48 i (真値: x = -1.0426 ±2.4791 i )
-
- ■参考文献
-
- ・布尾晃「計算尺・合理的使用法」(槙書店)
- 改版メモ
- ・2015/04/14 : 初版
-









