逆数を得る
- 基本的すぎてか、取説に載ってない場合もありますが、重要です。
-
- 【a】逆目盛の対数尺度を使う
-
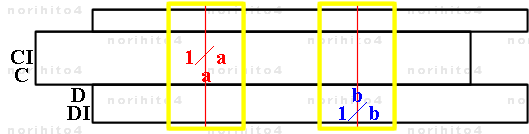
- C尺とCI尺, D尺とDI尺 (計算尺によっては、CFとCIF, AとAI, BとBI, KとKIも)は一方の数値にカーソルを合わせると
他方ではその逆数を示します。 カーソルの移動のみで連続的に逆数を得ることができます。
-
- h>C[a] → CI[1/a], h>D[b] → DI[1/b]
-
-
-
- 【b】固定尺と滑尺の同じ対数尺度を使う
-
- 固定尺と滑尺とに隣り合わせに配備された同じ対数尺の組合せは、互いの基線の位置で逆数の関係になってます。
-
- C尺とD尺の組合せを使います(他に計算尺によって CF尺とDF尺, A尺とB尺も)。
例えば、滑尺を動かしてC尺の基線をD尺のある数値 a に合わせると、D尺の基線はC尺の 1/a
を示します( CF, DF尺の場合は基線ではなく、1, 10 を使います)。
-
- C[i]>D[a] → C[1/a], D[i]>C[b] → D[1/b]
-

-
- ※ この手法は、DI尺が付いていない計算尺において、普通に計算するより最後に逆数をとるように計算する方が
計算尺操作が簡単な場合に有効です。
-
- 【c】LL+尺とLL-尺の組合せを使う
-
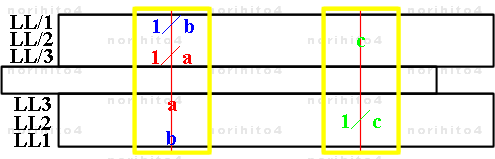
- LL3とLL/3尺, LL2とLL/2尺, LL1とLL/1尺, LL0とLL/0尺の組合せは C尺と CI尺のように逆数関係になっており、
カーソル操作のみで逆数を得ることができます。
- 特に、LL1〜LL0尺, LL/1〜LL/0尺 は 1 に近い数の逆数を精度良く得ることができます。
-
-
- ※ 通常、LL尺群での計算は位取りを自由にできませんが、この使用法においては位取りを
C, CI尺同様に任意に考えることができます。
-
- ※ 読みで 272(=e)〜368(=1/e) の範囲は 【a】,【b】 の1単位対数尺(C,D,CI,DI,CF,DF,CIF)による方法が
【c】 のLL尺群を使用するより精度が良く、その他の範囲は LL2〜LL0, LL/2〜LL/0 尺 を使用した方が精度が良いです
( A, B 尺, LL3, LL/3 尺は精度が悪いです)。 もちろん、計算尺の調整誤差を考慮しなければですが・・・。
-
-
- 【d】 1 に非常に近い数の逆数
-
- LL1〜LL0尺, LL/1〜LL/0尺 よりさらに 1に近い数(例えば 1.00032, 0.99993 など)の逆数を得るには、
以下の近似を筆算で行います。
- x を 1 に対して極めて小さい数とすると、1 に極めて近い数 1+x の逆数は、
-
- 1 /(1 + x) ≒ 1 - x
-
- と、1-x
に極めて近い数になります。
-
- 例: 1.000512 (x = 0.000512)
-
- 1 /1.000512 = 1 /(1 + 0.000512) = 1 /(1 - x) = 1 - x = 1 - 0.000512 = 0.999488
- 改版メモ
- 2007/09/18 : 一部修正。 図追加。 項目【d】追加。
- 2007/06/04 : 初版


