【解説】 5乗根 a^(1/5) の解法について

※ 問題「5乗根」の答えにも関係してます。この問題を自力で解きたい人は読まないでください。

　

■ 5乗根の解法手順（滑尺による数値の設定を 1回までに限定した場合）

　

　　　　h>A[a] 逆sl[i]>h find(x1,x2 | x1=x2) 【h>逆B[x1] ⇔ h>K[x2]】 → D[a^(1/5)]

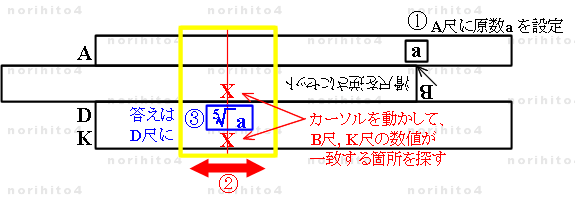
① 滑尺を上下逆に差込み、基線を A尺の a に合わせます。（このあと滑尺を動かしてはいけません。）

② カーソル線で逆さB尺と K尺の数値が一致する箇所を探します。
　（この数値は答えではありません。 a^(3/5) です。）

③ カーソル線下の D尺に a の 5乗根 a^(1/5) が得られます。

【注意】

　B尺とK尺の数値を一致させるときに、領域をきちんと合わさないと D尺に答えが出ません。

　例えば、K1,K2,K3領域に対し、B1,B2,B1領域を対応させ、数値を合わせます。

　下記に 0.000001 ＜ a ≦ 100000 における操作

　0.000001 ≦ a ≦ 0.00001: 逆sl[l.i]>A[a] h>【find 逆B1=K3】 → D[a^(1/5)]; 　
　0.00001 ≦ a ≦ 0.0001: 逆sl[r.i]>A[a] h>【find 逆B2=K1】 → D[a^(1/5)]; 　
　0.0001 ≦ a ≦ 0.000464: 逆sl[l.i]>A[a] h>【find 逆B2=K1】 → D[a^(1/5)]; 　
　0.000464 ≦ a ≦ 0.01: 逆sl[r.i]>A[a] h>【find 逆B1=K2】 → D[a^(1/5)]; 　
　0.01 ≦ a ≦ 0.0215: 逆sl[l.i]>A[a] h>【find 逆B1=K2】 → D[a^(1/5)]; 　
　0.0215 ≦ a ＜ 1: 逆sl[l.i]>A[a] h>【find 逆B2=K3】 → D[a^(1/5)]; 　
　1 ＜ a ≦ 46.4: 逆sl[r.i]>A[a] h>【find 逆B1=K1】 → D[a^(1/5)]; 　
　46.4 ≦ a ≦ 100: 逆sl[r.i]>A2[a] h>【find 逆B2=K2】 → D[a^(1/5)]; 　
　100 ≦ a ≦ 2154: 逆sl[l.i]>A[a] h>【find 逆B2=K2】 → D[a^(1/5)]; 　
　2154 ≦ a ≦ 10000（1万）: 逆sl[r.i]>A2[a] h>【find 逆B1=K3】 → D[a^(1/5)]; 　
　10000（1万） ≦ a ≦ 100000（10万）: 逆sl[l.i]>A[a] h>【find 逆B1=K3】 → D[a^(1/5)]; 　
　100000（10万）≦ a ≦1000000（100万）: 逆sl[l.i]>A[a] h>【find 逆B2=K1】 → D[a^(1/5)];

　B尺が 2単位尺、K尺が3単位尺であるため、対応する領域がずれていくことが分かります。

■解説

　

　この解法は、対数尺だけによる 5乗 a^5 の計算を逆行するイメージで得られます。

　対数尺だけによる 5乗の計算は色々考えられますが、尺度間での数値の移動（一度数値を読み取って他の尺度に設定し直す）を認めない場合は、

　h>D[a] CI[a]>h h>B[a] → A[a^5] ,　　h>A[a] CI[a]>h h>C[a] → A[a^5]

　等の方法がありますが、これらの操作を逆行して、滑尺操作 1回で、かつ、尺度間での数値の移動なしで 5乗根を求める操作を見いだすのは私には無理でした。

　次に、尺度間での数値の移動を利用した方法は、ISRG の Gary Flom さんのメッセージ #20044 にありました。

　これは、John St Clair さんのメッセージ #20040 の「滑尺とカーソルそれぞれ 1度の操作で、 1～100 の数の 5乗根を求めるにはどうしますか？」への Gary Flom さんの回答で、以下のような方法で 5乗根を求めています。

　まず、5乗の計算を、 a^2 * a^3 = a^5 として考えます。

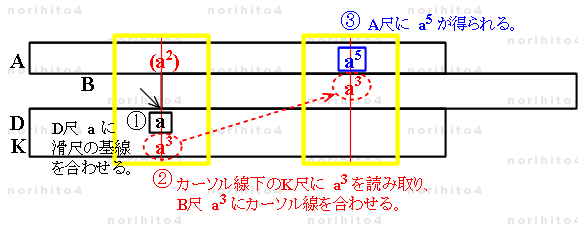
h>D[a] → A[a^2] , K[a^3]　：

　D尺 a にカーソル線を合わせると A尺に a^2, K尺に a^3 が得られます。

sl[i]>h h>B[a^3] → A[a^5]　：

　次に、カーソル線に滑尺基線を合わせ、B尺 a^3 にカーソル線を移動すると、A尺に a^5 が得られます。

この操作は、A, B尺で a^2 * a^3 = a^5 といった掛け算をしてるのと同じです。

sl[i]>A[a^2] h>B[a^3] → A[a^5]

　この操作を逆行したものが、Gary Flom さんの 5乗根の求め方で、下記・下図のようになります。

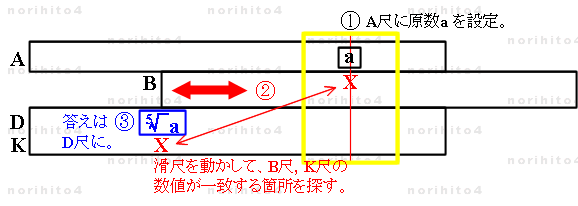
　　　　h>A[a] find(x1,x2 | x1=x2) 【B[x1]>h ⇔ sl[i]>K[x2]】 → D[a^(1/5)]

① カーソル線を A尺の a に合わせます。

② 滑尺を動かして、カーソル線下の B尺数値と滑尺基線上の K尺の数値が一致する箇所を探します。
　（この数値は答えではありません。 a^(3/5) です。）

③ 滑尺基線に対する D尺に a の 5乗根 a^(1/5) が得られます。

　Gary Flom さんは Sterling Decimal Trig Log-Log を使用したと言ってますので、K尺は本来 A尺の上に配置されてますが、いずれにしても K尺は滑尺から離れているため、滑尺基線で値を探すというのはちょっと苦しいです。カーソルがもう一つ欲しいところですね。

　最後に、本解法についてですが、Gary Flom さんの解法を大いに参考にしました。

　Gary Flom さんの 5乗根の解法では、カーソルを固定して滑尺を移動して a^(3/5) を探してましたが、これは、元となる 5乗の計算 a^2 * a^3 を A, B尺の基線法（カーソル法）で行っているためです。

　そこで私は、単純に、もしも BI尺があって、中合わせ法（滑尺法）で a^2 * a^3 を計算できるなら、 5乗根の計算は、滑尺を固定してカーソル線で BI尺, K尺の a^(3/5) を探せると思い、ヘンミ 40RK の滑尺を逆さに差し込んで検証してみました。

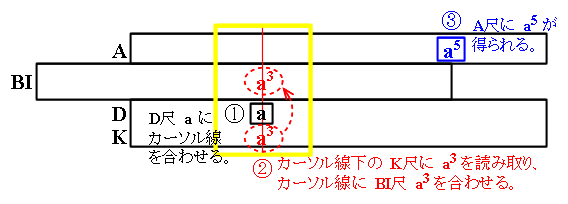
　BI尺を想定した計算尺での a^5 の計算方法は下記の通りです。

h>D[a] → K[a^3] （ , A[a^2]）　：

　D尺 a にカーソル線を合わせるとK尺に a^3 が得られます。
　（A尺には a^2 が得られてます。）

BI[a^3]>h → A[a^5] @sl[i]　：

　次に、カーソル線に BI尺 a^3 を合わせると、滑尺基線位置 A尺に a^5 が得られます。

　BI尺の代わりに滑尺を逆さに差して B尺を逆目盛にし、5乗の計算操作を逆行したものが、本解法による 5乗根の計算操作です。

　以下にダイヤグラムを再掲します。

　この方法によると、最終的にカーソル線下には、 A尺に a^(2/5) 、逆B尺と K尺に a^(3/5) 、そして D尺に a^(1/5) が得られます。